Что такое чёрная дыра
Если Солнце когда-нибудь станет таким телом, то его необходимо сжать до радиуса всего 9 км, а Землю и вовсе нужно сжать до размеров горошины.
 Теория струн допускает рождение чёрных дыр микроскопических размеров от столкновения двух частиц (например, протонов). При ударе возможно их сильное сжатие, достаточное для появления микроскопической черной дыры, но время жизни её ничтожно и опасности она не представляет. Большой взрыв вполне мог способствовать появлению этих объектов, потому что тогда плотность материи была очень высокой. Но небольшие дыры наверняка испарились, теряя массу посредством излучений и потоков частиц. До наших времён могли дожить лишь тела, массы которых были больше 1012 кг. Нынешний размер таких объектов сопоставим с протоном или нейтроном.
Теория струн допускает рождение чёрных дыр микроскопических размеров от столкновения двух частиц (например, протонов). При ударе возможно их сильное сжатие, достаточное для появления микроскопической черной дыры, но время жизни её ничтожно и опасности она не представляет. Большой взрыв вполне мог способствовать появлению этих объектов, потому что тогда плотность материи была очень высокой. Но небольшие дыры наверняка испарились, теряя массу посредством излучений и потоков частиц. До наших времён могли дожить лишь тела, массы которых были больше 1012 кг. Нынешний размер таких объектов сопоставим с протоном или нейтроном.
Горизонт событий
Чёрные дыры создают невероятные гравитационные поля, поэтому пространство и времени возле них сильно искажается.
Горизонтом событий называют границу, из которой не могут вырваться объекты даже со скоростью света. За очень малое время вещество за горизонтом событий сжимается в точку – сингулярность.В ней плотность и тяготение принимают бесконечные значения. Но всё это верно для обычного, макромира. Микромир ещё не имеет своей теории гравитации.
Что внутри чёрной дыры
Установлено, что внутри черной дыры — сингулярность. У нас пока нет инструментов для изучения этих объектов, зато есть пара увлекательных видеороликов 🙂
Интересные факты
- Время возле чёрных дыр протекает медленнее, нежели вдали от них. Если наблюдать за предметом, брошенным в этот объект, то движение предмета будет замедляться, а видимость его ослабляться. В конце он остановится и станет невидимым. Но если наблюдатель сам прыгнет туда, то мгновенно упадёт в центр дыры, а гравитационные силы разорвут его моментально. А увидит он всю жизнь вселенной, от рождения до смерти.
- Интересное свойство — после преодоления горизонта событий: чем сильнее вы будете сопротивляться гравитации чёрной дыры и стремиться улететь подальше, тем быстрее вы упадёте в неё. Тяжело себе такое представить, согласитесь…
- Неважно, что из себя представляло тело до сжатия, после этого процесса можно исследовать лишь три его параметра. Это электрический заряд, полная масса и момент импульса. Невозможно установить исходные параметры чёрной дыры – её форму, цвет, состав вещества.
- Всё, попадающее за горизонт событий, обязательно падает к центру, где находится сингулярность, имеющая бесконечную плотность. Это место, где уже не работают законы физики и классические концепции пространства и времени.
- Стивен Хоккинг сумел открыть испарения чёрных дыр. Крупные дыры будут испаряться очень долго — десятки и сотни миллиардов лет, а микроскопические — за доли секунды. Гипотетическое испарение, или испускание фотонов называют излучением Хокинга. Этот процесс имеет чисто теоретическое обоснование. Согласно теории, черные дыры образовавшиеся при рождении Вселенной и имеющие массы 1012кг, к нашему времени должны полностью испариться. Поскольку интенсивность испарения возрастает с уменьшением размера, то этот процесс должен закончиться взрывом. Пока такие взрывы астрономами не наблюдались.
- Классическая теория гравитации предполагает, что черную дыру невозможно ни уменьшить, ни уничтожить. Она может только увеличиваться. Из этого следует, что информация, попавшая внутрь недоступна для наружного наблюдателя.
- Никто не знает наверняка, что мы увидим, приблизившись к чёрной дыре. Но вполне возможно, что она не такая и чёрная. Вещество, летящее на её поверхность, разгоняется и разогревается, и, перед тем, как нырнуть за горизонт событий, должно светиться. Поэтому перед нами будет не круглый тёмный вырез в пространстве, а сияющий ореол, немного похожий на солнце в момент его полного затмения.
Сверхмассивные чёрные дыры
Все галактики имеют в своём центре чёрные дыры, включая и нашу. Такие выводы сделаны на основании наблюдений движения межзвёздного газа и близких звезд. Расчёты показывают, что объекты в центре галактики должны иметь громадные массы при небольших размерах. Получается, что центр любой галактики и есть чёрная дыра. И массы их – миллионы и миллиарды масс Солнца. Все наблюдаемые звёздные системы со свойствами чёрных дыр имеют массы 4 – 16 солнечных.
В нашей галактике за 12 млрд. лет её жизни должны были образоваться десятки миллионов этих суперплотных объектов. Астрономические наблюдения это подтверждают, но природа появления таких сверхгигантских чёрных дыр пока не ясна.Столкновение чёрных дыр
Если две чёрные дыры столкнутся, то должно произойти их слияние. Это событие будет сопровождаться излучением гравитационных волн. По величине такая энергия составит несколько процентов от суммарной массы дыр. И существование гравитационных волн было доказано в обсерватории LIGOLIGO — лазерно-интерферометрическая гравитационно-волновая обсерватория.Главная задача LIGO — экспериментальное обнаружение гравитационных волн космического происхождения. Эти волны впервые были предсказаны в общей теории относительности Эйнштейна в 1916 году, когда ещё не существовало технологий, необходимых для их обнаружения.
Многие сигналы — колебания звезд, еще какие-то — переводят в звуковую форму. Вот так жутковато выглядит звук слияния двух чёрных дыр:
Как их обнаружить
Обнаружить чёрную дыру возможно, если она входит в состав двойной системы, Например, в двойной системе одна из звезд взрывается, превращаясь в сверхновую. На оставшуюся звезду будет действовать гравитация соседки, следовательно вещество из звезды будет перетекать в чёрную дыру (она буквально будет «пожирать» звезду).
Вещество со звезды закрутится в спираль вокруг черной дыры, произойдёт его сильное уплотнение и разогрев. Нагрев будет продолжаться до возникновения волнового излучения в рентгеновском диапазоне, по характеру которого и можно понять параметры объекта. Также, черная дыра, пролетая возле звезды, отклоняет ее с обычной траектории своей колоссальной гравитацией, тем самым выявляя себя. Чёрные дыры, не имеющие напарника-звезду, также существуют в теоретических расчётах.

Как изучают
Изучают черные дыры в основном при помощи математического моделирования и физики. Если теоретические выкладки согласуются с наблюдениями и не противоречат доказанным фактам, гипотеза превращается в общепризнанную теорию. Вот видео где это подробно рассмотрено:
light-science.ru
Характеристика пространства и времени в черных дырах

Черная дыра — одна из наиболее таинственных тем общей теории относительности А. Эйнштейна. У черных дыр любопытная история, ведь они подкинули ученым полным-полно сюрпризов, даровавших нам лучшее понимание характеристик пространства и времени. Начнем с теории всемирного тяготения Ньютона. Всю мощь гравитации мы переживаем прямо тут, на поверхности Земли. Если подкинуть какой-то предмет, он упадет под действием земного притяжения. Но реально ли сделать так, чтобы подкинутый предмет обратно уже не вернулся? Реально. Если пустить его со скоростью, превышающей вторую космическую скорость (около 11 км/с), он оставит гравитационное поле планеты. На этот параметр влияет масса и радиус земного шара. Если бы Земля при текущем радиусе была тяжелее или была бы меньшего радиуса при нынешней массе, «скорость выхода» была бы выше. Зарождается вопрос: а что если плотность и масса космического тела настолько огромны, что скорость выхода из его поля притяжения выше скорости света? Подобное тело будет казаться стороннему наблюдателю совершенно черным, ведь даже свет его покинуть не в состоянии. К примеру, звезда с радиусом меньше, чем
где GN — постоянная Ньютона, а с — скорость света в вакууме, будет казаться совершенно черной.
где GN — постоянная Ньютона, а с — скорость света в вакууме, будет казаться совершенно черной.
Тем, кто не ориентируется в математических формулах, приведу парочку примеров. Для того чтобы тело, равное по массе Земле, обратилось в черную дыру, ему необходимо обладать радиусом до одного сантиметра. Радиус объекта с массой Солнца должен быть менее километра. Об этом ещё в XVIII веке говорил Пьер-Симон Лаплас, чему в те времена никто не придал никакого значения.
С возникновением в 1905 году специальной теории относительности люди осознали, что скорость света в вакууме не является типовой. Это вселенская грань: ничто не способно перемещаться быстрее света. ТО (теория относительности) Эйнштейна говорит о том, что пространство и время очень взаимосвязаны. Для объектов, движущихся друг относительно друга, время идет с неодинаковой скоростью. Допустим вы стоите на улице и глядите на проезжающие мимо автомобили. Для их водителей время бежит немного медленнее, нежели для вас. К примеру, вы видите, что два светофора в разных концах улицы синхронно переключаются на красный. Для водителей же это происходит не синхронно, что получается, когда мы учитываем время, затраченное на достижение света светофора глаз наблюдателей. И для вас, и для водителей свет движется с одинаковой быстротой, но время для них идет медленнее. Значит, время относительно, а скорость света безусловна. Это перечит нашим подсознательным взглядам на мир, потому что подобный эффект на нас совершенно не влияет, ведь мы существуем на скоростях, невероятно отдаленных от скорости света, а время считаем не с абсолютной точностью. Но при всем при том в ускорителях элементарных частиц данный эффект замечается регулярно. При скоростях, приближающихся к скорости света, частицы существуют существенно дольше.
Характеристики пространства и времени сливаются в общую концепцию пространства- времени. Время воспринимается различно двумя наблюдателями, движущимися друг относительно друга. Но они воспринимают одинаковое пространство-время. Существуют точные формулы, дающие возможность нам объединить наблюдения этих двух наблюдателей.
Но возвратимся к притяжению, которое имеет крайне значимое свойство, обнаруженное еще Галилеем: все тела падают одинаково, если не считать сопротивление воздуха. В вакууме бумажка и булыжник упадут на землю в одно и то же время. С другими силами это не так. В теории всемирного тяготения Ньютона фактор, из-за которого все тела движутся под влиянием притяжения в равной степени, объясняется тем, что сила тяготения соразмерна массе тела. Порой это именуют «принципом эквивалентности».
Эйнштейн понял, что теория Ньютона противоречит ТО, так как соответственно Ньютону гравитационное воздействие тел друг на друга происходит в один миг. В 1915 году Эйнштейн разрешил проблему так, что из решения естественным путем следует и принцип эквивалентности. Новую теорию Эйнштейн окрестил общей теорией относительности (ОТО). Он допустил, что притяжение рождается по причине искажения пространства-времени. В искаженном пространстве-времени частицы движутся по наименьшим траекториям. Изначально параллельные линии этих траекторий в искаженном пространстве-времени могут сближаться. Взять, к примеру, два земных меридиана, параллельных на перекрещивании с экватором, но при отдалении от него они будут сходиться, пока не перехлестнутся на Северном полюсе. Характеристика пространства-времени зависит от материи, двигающейся внутри него. ОТО имеет в виду, что ход времени зависит от притяжения. Таким образом, жильцы разных этажей одного дома воспринимают течение времени неодинаково. Для жильца первого этажа оно протекает медленнее, чем для жильца последнего этажа. Для наших зданий это явление практически незаметно. Основное, что необходимо усвоить: большие объекты затягивают пространство-время на себя. Поэтому рядом с ними время движется медленнее, чем на расстоянии от них.

Физики постоянно стараются вначале рассмотреть элементарные ситуации. Вследствие этого в 1916 году, сразу после открытия ОТО, молодой физик Карл Шварцшильд отыскал элементарное сферически симметричное решение уравнений Эйнштейна. Оно характеризует частный случай искажения геометрии пространства-времени под влиянием точечной массы. Но вместо геометрии лучше сосредоточимся на ином аспекте: темпе хода стационарных часов. Часы на Солнце будут идти в 0,000001 раз медленнее, чем на расстоянии от него. На нейтронной звезде часы идут со скоростью 70% от скорости часов вдалеке от нее. Перед нами заметный эффект расхождения во времени. Решение Шварцшильда предсказывает остановку часов в «центре» точечной массы. Сначала физики посчитали это «нефизическим» парадоксом, результатом чрезмерно упрощенного рассмотрения.
Последующие расчеты выявили, что речь в решении Шварцшильда идет не сколько об каком-то условном «центре», сколько о целой идеальной сфере. Объект, проходящий через рубежи этой сферы и оказывающийся внутри, не замечает ничего противоестественного — для него время идет как и раньше. Однако для наблюдателей вне сферы, получающих сигналы от двигающегося в сфере объекта, любые сигналы от него будут упорно тормозиться, пока не пропадут при пересечении границ сферы. Поверхность, где стационарные часы тормозятся до нуля, называют сферой Шварцшильда или «горизонтом». Вернуться отсюда невозможно. Объект, попавший за горизонт, назад уже не выкарабкается и будет неминуемо съеден сингулярностью в ее центре. «Сингулярность» — это участок сверхвысокого искажения пространства-времени, и объект в ней просто-напросто пропадет и будет расплющен громадной гравитационной силой.
Черные дыры могут создаваться в ходе астрофизических явлений, когда у звезд с массой заметно выше Солнечной исчерпывается термоядерное топливо, и они падают внутрь себя под влиянием притяжения. Существует множество подобных наблюдений, говорящих о существовании таких черных дыр во Вселенной. С позиции астрофизики открытые черные дыры сортируются на два вида. Первый — черные дыры, сформировавшиеся из-за коллапса огромных звезд и располагающие надлежащей массой. Так как черные дыры выглядят действительно черными, заметить их очень трудно. Если повезет, возможно разглядеть только шлейф газа, завлекаемого внутрь дыры. Ускоряясь при падении, газ греется и распространяет специфическое излучение, которое мы только и можем заметить. Родником газа здесь служит другая звезда, образующая парную систему с черной дырой и вращающаяся совместно с ней вокруг центра масс двойной звездной системы. Иначе говоря, сперва мы располагали обычной двойной звездой, после чего одна из звезд в процессе гравитационного коллапса стала черной дырой. Вслед за этим, черная дыра начинает затягивать газ с поверхности горячей звезды. Второй тип — это куда более массивные черные дыры в центрах галактик. Их масса превосходит массу Солнца в миллиарды раз. И снова, падая на подобные черные дыры, материя греется и излучает свойственное излучение, которое затем достигает Земли. Это излучение мы и можем обнаружить. Предполагается, что все крупные галактики, включая нашу, содержат в центре собственную черную дыру.
Но основополагающим объектом нашего разговора будет не астрофизика черных дыр, а изучение их воздействия на структуру и характеристику пространства-времени.
По теории Эйнштейна черная дыра являет собой глубокий провал в пространстве-времени, падение в который необратимо.
У черных дыр весьма занимательные качества. После коллапса звезды в черную дыру ее особенности будут характеризоваться лишь двумя параметрами: массы и углового времени вращения. Это значит, что черные дыры исполняют роль универсальных объектов, их свойства не зависят от вещества, из коего они сформированы. При каждом химическом составе вещества исходной звезды качества черной дыры будут одинаковыми. Черные дыры повинуются лишь законам теории гравитации — и никаким другим.

Ещё одно свойство состоит в следующем: допустим, вы следите за явлением, где участвует черная дыра. В частности можно проанализировать процесс столкновения двух черных дыр. В итоге из двух черных дыр сформируется одна более массивная. Это явление может происходить с испусканием гравитационных волн, и уже есть детекторы для их выявления и замера. Такой процесс в теории рассчитать довольно трудно: для этого надо вывести сложную систему дифференциальных уравнений. Тем не менее, существуют и тривиальные теоретические выводы. Площадь сферы Шварцшильда получившейся черной дыры неизменно превышает сумму площадей поверхностей двух отправных черных дыр. Значит, при объединении черных дыр площадь их поверхности увеличивается стремительнее массы. Это «теорема площадей», которая обоснована С. Хокингом в 1970 году.
Черные дыры и квантовая механика.
Ещё один подарок ожидал исследователей, когда они начали изучать квантовые эффекты. В квантовой механике вакуум — это не только абсолютное отсутствие элементарных частиц. Вакуум — это очень интересное состояние пространства, в котором все время появляются и немедленно аннигилируют пары «частица-античастица». В спрямленном пространстве чистым выходом в виде завязавшихся в вакууме частиц мы не обладаем в силу закона сохранения энергии. Частицы взаимно аннигилируются, ещё не успев появиться на свет. В 1974 году С. Хокинг привел доказательства, что поблизости горизонта это не так. Есть отличная от нуля вероятность рождения пары частиц, немедленно оказывающихся по разные края безгранично тонкого горизонта, при этом закон сохранения энергии не нарушается, ведь частица за пределами горизонта владеет с точки зрения стороннего наблюдателя положительной энергией, а частица внутри горизонта — отрицательной (с точки же зрения наблюдателя внутри сферы Шварцшильда всё будет противоположно). Термическое распределение распространяемых частиц отвечает температуре, обратно пропорциональной массе черной дыры. Даже для черных дыр звездной массы температура так недалека от абсолютного нуля, что это проявление зафиксировать практически нельзя. Но если черная дыра довольно длительное время была бы в совершенном вакууме, то с помощью эффекта Хокинга она понемногу бы утрачивала массу сквозь излучение порождающихся на поверхности частиц. Лишаясь массы, черная дыра нагревается. Черная дыра с массой около 1019 кг (масса большого горного хребта) нагреется до температуры в несколько тысяч градусов и станет казаться белой. Однако мощность этого излучения будет составлять не более милливатта, и зафиксировать его все так же почти нельзя. Но с уменьшением массы обособленной черной дыры повышается её температура и ускоряется её «испарение», пока, скорее всего, она не испарится целиком. Фактически, если бы можно было стиснуть до плотности черной дыры лишь несколько килограммов материи (чего на практике добиться нельзя), подобная черная дыра исчезла бы меньше, чем за одну миллисекунду, а энергии она выделила бы больше водородной бомбы.
Существование этого теплового излучения у черных дыр немедленно создает два вопроса: 1) факторы роста энтропии черной дыры; 2) информационный парадокс.

Энтропия черных дыр.
Энтропия является сходным температуре термином. Она показывает количественное отражение меры хаотичности движения молекул. Законы термодинамики разрешают связать энтропию с температурой, массой и объемом, вследствие чего её можно вычислить, не вдаваясь в микроскопические элементы структуры системы. Хокинг и Бекенштейн (Bekenstein) обнаружили, что энтропия черной дыры соразмерна зоне её горизонта, разделенной на квадрат т. н. гравитационной длины Планка в 10–33 см. Для черной дыры макроскопических масштабов роль энтропии просто невероятна. И все же законов термодинамики в этой ситуации, пожалуй, никто не отменял, и они все так же работают, учитывая нескончаемый «вклад» незримых недр черной дыры в её энтропию. Результаты эти весьма озадачивают, в первую очередь от того, что полностью не ясно, из чего формируется энтропия черной дыры, так как очевидных составляющих, каковые своим беспорядочным движением способствовали бы безграничному росту энтропии, в черной дыре не имеется. Или, как минимум, мы не имеем возможности увидеть их «за пределами», поскольку нам мерещится всего-навсего по-настоящему «черная» дыра — глубокий провал в материи пространства-времени, и чтобы выяснить, из каких «составляющих» она построена, нужно разыскать хотя бы фундаментальные составные части, на которые можно разделить геометрию пространства-времени.
Очень любопытно и то, что энтропия черной дыры соразмерна её площади (квадрату радиуса), а не объему (кубу радиуса). В начале 1990-х годов Хофт и Зюскинд допустили, что в теории, связывающей квантовую механику и гравитацию, число элементарных составляющих, нужных для полной характеристики системы, пропорционально площади опоясывающей поверхности, куда она заключена. А это значит, что строение пространства-времени очень различно со структурой твёрдого тела, в каковом количество подобных элементарных составляющих (материальных точек или атомов) возрастает пропорционально её объему, а вовсе не площади. Практически, это ограничение энтропии поверхностью сферы не выглядит излишне принципиальным, но теоретически оно лихо переворачивает представления о мире, ведь оказывается вероятным охарактеризовать замкнутую пространственно-временную область только лишь по поведению звеньев, размещенных на её наружной границе.
Информационный парадокс.
Уже говорилось, что происхождение чёрной дыры бывает разнообразным, но на её качества это не влияет. Как правило, в физике при фазовом переходе или прочем переустройстве от начального состояния материи зависит её итоговая характеристика. Порой отличия почти незаметны, но они наличествуют. Возьмём две совершенно одинаковые тарелки, нацарапаем на первой букву А, а на второй — Б, потому расколотим обе на маленькие кусочки. Казалось бы, итог идентичен — две кучи осколков на полу. Но скрупулезно рассмотрев горы битого фарфора, мы сможем выяснить, на какой тарелке какая буква была.
А теперь представим, что одну тарелку швырнули в чёрную дыру. По тому, что нам известно на нынешний момент, вещество черной дыры вместе с останками тарелки улетучится в форме излучения Хокинга. По теории это будет термическое излучение, не зависящее от начального статуса ни черной дыры, ни оказавшейся внутри тарелки. Следовательно, получить сведения о том, что за буква была нацарапана на тарелке, уже никогда не получится.
Это может выглядеть настоящей академической казуистикой. Мы же все время что-то да забываем в повседневной жизни, и не видим тут ничего неестественного. А проблема на самом деле жутко серьезна, так как квантовая механика говорит, что законы, контролирующие это явление, таковы, что подобные данные обязаны быть восстановимы. Отсюда разрешение вопроса сохранения информации нужно с точки зрения создания внутренне непротиворечивой квантовой теории гравитации. Информационный парадокс должен найти решение в границах настоящей теории.
Многие известные физики считали это неосуществимым. Они полагали, что любая информация в черной дыре пропадает навсегда, и хотели отречься от Великого объединения теории взаимодействий в границах квантово-механических представлений, и от квантовой механики, так как она означает утопический закон сохранения информации.
Но дальнейшее постижение проблемы повлекло формирование теории струн в физике элементарных частиц.
Теория струн.
Квантовая механика и гравитационная теория в границах ОТО ладят друг с другом из рук вон плохо. На практике, в будничной жизни, квантовая теория гравитационного взаимодействия не применима, ведь процессы, с которыми приходится иметь дело, характеризуются или гравитационными силами, когда квантово-механические явления не обнаруживаются, или наоборот. Но если нас интересует порождение Вселенной и явления, проистекавшие сразу следом за Большим Взрывом, универсальная и непротиворечивая концепция становится необходимостью.
Этой концепцией стала теория струн, где получилось слить воедино квантово-механические и гравитационные взаимодействия. Пока неизвестно насколько точна эта теория, но ничего лучше неё на данный момент не имеется. Мы не будем затрагивать тему о происхождении столь интересного названия теории. Главное — понять, что это квантовая теория гравитации.

Чёрные дыры в рамках теории струн.
С помощью теории струн появилась возможность изучать внутреннее устройство черных дыр. Иногда можно получить изображение микроструктуры черной дыры. Легче всего разобраться в конструкции черных дыр, существующих в пространственно-временном континууме устойчивой отрицательной кривизны. Эти пространственно-временные континуумы — элементарное обобщение типичного спрямленного пространства с нулевой кривизной. Пространственно-временные континуумы с отрицательной кривизной обладают замкнутой чертой в бесконечности. Частица долетает до бесконечно удаленной грани и обратно за конечное время, и это на самом деле вероятно вследствие разнородности хода времени — оно ускоряется при удалении от отправной точки.
В 1997 году я предположил, что все гравитационные физические явления в этом пространстве можно выразить через теорию взаимодействия обычных частиц, размещенных на его границе. Эта идея досконально изучена многими теоретиками. Детали очень трудны для понимания, но главный момент заключается вот в чем: теория гравитации, которую мы пока не полностью постигли, сводится к теории взаимодействия обычных частиц на поверхности сферы, которую мы вполне осмыслили. Эта смежная теория гравитации повинуется позициям квантовой механики.
Термодинамическая характеристика черной дыры обозначена исключительно температурой частиц в её граничном покрове. Следовательно, энтропия чёрной дыры равна только общей энтропии частиц. Сами же пограничные частицы принадлежат к «элементарным квантам» пространственно-временной геометрии.
Строение пространства-времени.
Эти теории сильно касаются взглядов на строение пространства-времени. Следует заметить, что все началось с теории поведения частиц на сферической плоскости, ограничивающей черную дыру, то есть имели дело с трехмерными пространственно-временными измерениями, а завершили четырехмерной теорией гравитации. Выходит, одно измерение появилось почти из ниоткуда! На самом деле оно родилось из взаимодействий частиц в 2+1 измерениях.
Из этого следует, что пространство-время — не самое фундаментальное понятие. Оно возникает из других фундаментальных понятий, а законы действуют на удалении наблюдателя от объекта. Определение пространства-времени при анализе в очень микроскопических масштабах лишается смысла. И получается, что на данном уровне основной является концепция слоя пограничных частиц, а само пространство-время — проявление их коллективных характеристик.
Если бы мы обитали в пространстве-времени с минусовой кривизной, то для уяснения всего творящегося во Вселенной хватило бы адекватной концепции пограничного слоя, обрисовывающего поведение частиц в нём.
Судя по существующим данным, в макроскопических масштабах пространство-время Вселенной обладает неотрицальной кривизной. На сегодня неведомо, есть ли вероятность для аналогичного описания гравитационных полей в пространстве-времени с положительной кривизной. Такая характеристика, если бы получилось её отыскать, убила бы вопросы сингулярности Большого взрыва…
www.the-submarine.ru
туннели сквозь пространство и время. Гиперпространство
Черные дыры: туннели сквозь пространство и время
Черные дыры с недавних пор завладели воображением широкой публики. Исследованию этого странного предположения Эйнштейна, финальной стадии смерти коллапсирующей звезды, посвящены книги и документальные фильмы. Парадокс, но публика по-прежнему не подозревает о самой, пожалуй, необычайной особенности черных дыр — что они могут служить воротами в другую вселенную. Более того, в научном сообществе активно высказываются предположения о способности черных дыр открывать туннели во времени.
Для того чтобы понять, что такое черные дыры и как трудно отыскать их, следует сначала выяснить, почему сияют звезды, как они растут и как в конце концов погибают. Звезда рождается, когда огромное облако водорода, размерами многократно превосходящее нашу Солнечную систему, медленно сжимается под действием силы гравитации. Эта сила, сжимающая газ, постепенно нагревает его, поскольку гравитационная энергия преобразуется в кинетическую энергию атомов водорода. В обычных условиях отталкивающего заряда протонов в водороде достаточно, чтобы атомы оставались обособленными. Но в определенный момент, когда температура повышается до 10–100 млн кельвинов, кинетическая энергия протонов (ядер водорода) преодолевает электростатическое отталкивание, и они врезаются друг в друга. Тогда сила ядерного взаимодействия одерживает верх над электромагнитной силой, и два ядра водорода «сливаются», образуя гелий и выделяя огромные количества энергии.
Другими словами, звезда — это ядерная печь, в которой сгорает топливо — водород и образуется ядерная «зола» — отходы в виде гелия. Кроме того, звезда — случай шаткого равновесия между силой гравитации, стремящейся полностью уничтожить звезду, и силой ядерного взаимодействия, обладающей мощностью триллионов водородных бомб, которая стремится разорвать звезду. Расходуя свое ядерное топливо, звезда достигает зрелости и старости.
Для того чтобы понять, как в ходе ядерной реакции выделяется энергия, и выяснить, какие жизненные этапы проходит звезда, прежде чем стать черной дырой, обратимся к рис. 10.1, на котором представлен один из наиболее важных графиков современной науки, иногда называемый кривой энергии связи. На горизонтальной оси отражена атомная масса различных элементов — от водорода до урана. На вертикальной оси — грубо говоря, приблизительный средний «вес» каждого протона в ядре. Обратите внимание: протоны водорода и урана в среднем тяжелее, чем протоны других элементов в центре графика.

Рис. 10.1. Средняя масса каждого протона менее тяжелых элементов, таких как водород и гелий, сравнительно велика. Таким образом, если в звезде из водорода получается гелий, остается избыток массы, который преобразуется в энергию соответственно формуле Эйнштейна E = mc2. Благодаря этой энергии светят звезды. Но по мере того, как в реакцию вступают все более и более тяжелые элементы, особенно когда дело доходит до железа, получать больше энергии уже не удается. Тогда звезда схлопывается с гигантским выбросом тепла, в итоге возникает сверхновая. Колоссальный взрыв разрывает звезду и «осеменяет» межзвездное пространство, в котором образуются новые звезды. После этого процесс начинается сначала, как в автомате для игры в пинбол.
Наше Солнце — обыкновенная желтая звезда, состоящая главным образом из водорода. Как и при Большом взрыве, в ней из водорода образуется гелий. Но, поскольку протоны водорода тяжелее протонов гелия, возникает избыток массы, который преобразуется в энергию в соответствии с формулой Эйнштейна E = mc2. Эта энергия и связывает ядра вместе. Кроме того, энергия высвобождается при образовании гелия из водорода. Вот почему солнце светит.
Но за миллиарды лет водород постепенно расходуется, в желтой звезде накапливается слишком много гелия, и ядерная печь прекращает работу. Когда это происходит, гравитация наконец одерживает верх и уничтожает звезду. При резком увеличении температуры звезда раскаляется достаточно, чтобы сжечь избыток гелия и преобразовать его в другие элементы, такие как литий и углерод. Обратим внимание, что энергия продолжает выделяться по мере снижения кривой в сторону более тяжелых элементов. Иными словами, горение гелия все еще возможно (точно так же обычная зола при определенных условиях может продолжать гореть). Несмотря на существенное уменьшение размера звезды, ее температура довольно высока, а внешняя оболочка значительно увеличивается в размерах. В сущности, когда наше Солнце исчерпает запасы водорода и начнет сжигать гелий, внешняя оболочка Солнца достигнет орбиты Марса. Возникнет так называемый красный гигант. Разумеется, это означает, что в процессе его возникновения Земля превратится в пар. Таким образом, кривая предсказывает окончательную участь Земли. Поскольку возраст нашего Солнца средний, т. е. ему примерно 5 млрд лет, пройдет еще 5 млрд лет, прежде чем оно поглотит Землю. (По иронии судьбы, Земля родилась из того же вихревого газового облака, из которого возникло наше Солнце. В настоящее время физики высказывают предположение, что Земля, созданная вместе с Солнцем, воссоединится с ним.)
И наконец, когда будет израсходован гелий, ядерная печь снова прекратит работу, и гравитация уничтожит звезду. Красный гигант сожмется и станет белым карликом — миниатюрной звездой, сократившейся примерно до размеров планеты Земля[112]. Белые карлики светят слабо, так как относятся к нижней части кривой, которой соответствует совсем небольшой избыток энергии согласно формуле E = mc2. Белый карлик сжигает то немногое, что остается на нижней части кривой.
Наше Солнце в конце концов превратится в белого карлика и на протяжении миллиардов лет будет медленно умирать, так как истощит все свои запасы ядерного топлива. В итоге оно станет темной, выгоревшей карликовой звездой. Однако считается, что если звезда обладает достаточной массой (в несколько раз превышающей массу нашего Солнца), то большинство элементов, содержащихся в белом карлике, будут по-прежнему участвовать в реакциях с образованием все более тяжелых элементов и со временем дело дойдет до железа. Излишки массы уже не будут давать энергии, ядерная печь прекратит работу. Гравитация вновь окажется сильнее и будет сжимать звезду, пока температура не увеличится сразу в тысячу раз, достигая триллионов градусов. В этот момент железное ядро сжимается, а наружная оболочка белого карлика разрушается, процесс сопровождается самым мощным в галактике выбросом энергии и образованием взрывающейся звезды — сверхновой. Всего одной сверхновой достаточно, чтобы на время затмить целую галактику со 100 млрд звезд.
После взрыва сверхновой мы обнаруживаем совершенно мертвую звезду — нейтронную звезду размером с Манхэттен. Плотность составляющих нейтронной звезды настолько велика, что, грубо говоря, нейтроны «трутся» друг о друга. Хотя нейтронные звезды почти невидимы, их можно обнаружить с помощью приборов. Вращаясь, они распространяют излучение, так что действуют как космические маяки. Мы видим их как мерцающие звезды, или пульсары. (Этот сценарий выглядит, как научная фантастика, тем не менее свыше 400 пульсаров было обнаружено с тех пор, как их открыли в 1967 г.)
Компьютерные вычисления показали, что большинство элементов, более тяжелых, чем железо, могут синтезироваться при температурах и давлении, характерных для сверхновой звезды. Когда звезда взрывается, в космический вакуум выбрасывается уйма «звездного мусора», состоящего из тяжелых элементов. Этот «мусор» в итоге смешивается с прочими газами, пока не накопится достаточное количество водорода, чтобы процесс гравитационного сжатия начался опять. Из газопылевых облаков, изобилующих тяжелыми элементами, рождаются звезды второго поколения. Некоторые из этих звезд (такие как наше Солнце) окружены планетами, содержащими тяжелые элементы.
Так разрешается давняя загадка космологии. Наши тела состоят из элементов, более тяжелых, чем железо, но наше Солнце не настолько горячее, чтобы создать такие элементы. Если Земля и атомы нашего тела возникли из того самого газового облака, откуда тогда в нашем теле взялись тяжелые элементы? Вывод однозначен: тяжелые элементы нашего тела были синтезированы в сверхновой звезде, которая взорвалась до появления нашего Солнца. Другими словами, некая безымянная сверхновая звезда взорвалась миллиарды лет назад, породив исходное газовое облако, из которого и образовалась наша Солнечная система.
Эволюцию звезды можно представить в виде автомата для игры в пинбол, как на рис. 10.1, имеющего форму кривой энергии связи. Шар начинает движение сверху, перескакивая от водорода к гелию, от более легких элементов к более тяжелым. При каждом его скачке по кривой появляется звезда другого типа. И наконец, шар достигает нижней части кривой, где находится железо, и в результате взрыва рождается сверхновая звезда. Затем звездное вещество опять собирается в новую звезду, богатую водородом, и процесс «игры в пинбол» возобновляется.
Отметим, однако, что существуют два способа движения шара вниз по кривой. Это движение может начаться с другой стороны кривой, с урана, и достигнуть дна единственным скачком, с расщеплением ядра урана. Поскольку средняя масса протонов таких продуктов деления, как цезий и криптон, меньше средней массы протонов урана, избыток массы преобразуется в энергию согласно формуле E = mc2. Это и есть источник энергии атомной бомбы.
Таким образом, кривая энергии связи не только объясняет рождение и смерть звезд и возникновение элементов, но и делает возможным существование водородной и атомной бомб! (Ученых часто спрашивают, можно ли создать ядерные бомбы помимо атомных и водородных. Как видно из кривой энергии связи, ответ на этот вопрос отрицательный. Отметим, что кривая исключает возможность создания кислородной или железной бомбы. Эти элементы расположены вблизи нижней части кривой, поэтому избытка массы не хватит для бомбы.
А упоминающиеся в прессе бомбы вроде нейтронной — это разновидности урановой и водородной бомб.)
Когда впервые слышишь историю жизни звезд, невольно относишься к ней скептически. Ведь никто же не мог прожить 10 млрд лет и стать свидетелем эволюции звезд. Но, поскольку звезд в небе бесчисленное множество, несложно увидеть звезды почти на всех этапах их эволюции. (К примеру, в 1987 г. сверхновая звезда, которую можно было наблюдать невооруженным глазом в южном полушарии, обеспечила нас множеством астрономических данных, соответствующих теоретическим предположениям о схлопывающемся карлике с железным ядром. Кроме того, остаток великолепной сверхновой звезды, которую наблюдали древнекитайские астрономы 4 июля 1054 г., в настоящее время идентицифирован как нейтронная звезда.)
Вдобавок наши компьютерные программы стали настолько точными, что мы в принципе можем численно прогнозировать порядок звездной эволюции. Когда-то у меня был сосед-аспирант, специализировавшийся на астрономии. Он неизменно уходил рано утром и возвращался поздно вечером. Перед уходом говорил, что ставит звезду в духовку, чтобы увидеть, как она растет. Поначалу я думал, что он шутит. Но, когда я стал расспрашивать его, он со всей серьезностью объяснил, что закладывает звезду в компьютер и весь день наблюдает за тем, как она эволюционирует. Поскольку уравнения термодинамики и термоядерных реакций хорошо известны, остается лишь задать определенную массу водорода и дождаться, когда компьютер представит эволюцию этого газа в численном виде. Таким способом можно убедиться, что наша теория звездной эволюции воспроизводит известные стадии жизни звезды, которые мы видим в телескопы.
Поделитесь на страничкеСледующая глава >
fis.wikireading.ru
туннели сквозь пространство и время — Мегаобучалка
Черные дыры с недавних пор завладели воображением широкой публики. Исследованию этого странного предположения Эйнштейна, финальной стадии смерти коллапсирующей звезды, посвящены книги и документальные фильмы. Парадокс, но публика по-прежнему не подозревает о самой, пожалуй, необычайной особенности черных дыр — что они могут служить воротами в другую вселенную. Более того, в научном сообществе активно высказываются предположения о способности черных дыр открывать туннели во времени.
Для того чтобы понять, что такое черные дыры и как трудно отыскать их, следует сначала выяснить, почему сияют звезды, как они растут и как в конце концов погибают. Звезда рождается, когда огромное облако водорода, размерами многократно превосходящее нашу Солнечную систему, медленно сжимается под действием силы гравитации. Эта сила, сжимающая газ, постепенно нагревает его, поскольку гравитационная энергия преобразуется в кинетическую энергию атомов водорода. В обычных условиях отталкивающего заряда протонов в водороде достаточно, чтобы атомы оставались обособленными. Но в определенный момент, когда температура повышается до 10–100 млн кельвинов, кинетическая энергия протонов (ядер водорода) преодолевает электростатическое отталкивание, и они врезаются друг в друга. Тогда сила ядерного взаимодействия одерживает верх над электромагнитной силой, и два ядра водорода «сливаются», образуя гелий и выделяя огромные количества энергии.
Другими словами, звезда — это ядерная печь, в которой сгорает топливо — водород и образуется ядерная «зола» — отходы в виде гелия. Кроме того, звезда — случай шаткого равновесия между силой гравитации, стремящейся полностью уничтожить звезду, и силой ядерного взаимодействия, обладающей мощностью триллионов водородных бомб, которая стремится разорвать звезду. Расходуя свое ядерное топливо, звезда достигает зрелости и старости.
Для того чтобы понять, как в ходе ядерной реакции выделяется энергия, и выяснить, какие жизненные этапы проходит звезда, прежде чем стать черной дырой, обратимся к рис. 10.1, на котором представлен один из наиболее важных графиков современной науки, иногда называемый кривой энергии связи. На горизонтальной оси отражена атомная масса различных элементов — от водорода до урана. На вертикальной оси — грубо говоря, приблизительный средний «вес» каждого протона в ядре. Обратите внимание: протоны водорода и урана в среднем тяжелее, чем протоны других элементов в центре графика.
Рис. 10.1. Средняя масса каждого протона менее тяжелых элементов, таких как водород и гелий, сравнительно велика. Таким образом, если в звезде из водорода получается гелий, остается избыток массы, который преобразуется в энергию соответственно формуле Эйнштейна E = mc2. Благодаря этой энергии светят звезды. Но по мере того, как в реакцию вступают все более и более тяжелые элементы, особенно когда дело доходит до железа, получать больше энергии уже не удается. Тогда звезда схлопывается с гигантским выбросом тепла, в итоге возникает сверхновая. Колоссальный взрыв разрывает звезду и «осеменяет» межзвездное пространство, в котором образуются новые звезды. После этого процесс начинается сначала, как в автомате для игры в пинбол.
Наше Солнце — обыкновенная желтая звезда, состоящая главным образом из водорода. Как и при Большом взрыве, в ней из водорода образуется гелий. Но, поскольку протоны водорода тяжелее протонов гелия, возникает избыток массы, который преобразуется в энергию в соответствии с формулой Эйнштейна E = mc2. Эта энергия и связывает ядра вместе. Кроме того, энергия высвобождается при образовании гелия из водорода. Вот почему солнце светит.
Но за миллиарды лет водород постепенно расходуется, в желтой звезде накапливается слишком много гелия, и ядерная печь прекращает работу. Когда это происходит, гравитация наконец одерживает верх и уничтожает звезду. При резком увеличении температуры звезда раскаляется достаточно, чтобы сжечь избыток гелия и преобразовать его в другие элементы, такие как литий и углерод. Обратим внимание, что энергия продолжает выделяться по мере снижения кривой в сторону более тяжелых элементов. Иными словами, горение гелия все еще возможно (точно так же обычная зола при определенных условиях может продолжать гореть). Несмотря на существенное уменьшение размера звезды, ее температура довольно высока, а внешняя оболочка значительно увеличивается в размерах. В сущности, когда наше Солнце исчерпает запасы водорода и начнет сжигать гелий, внешняя оболочка Солнца достигнет орбиты Марса. Возникнет так называемый красный гигант. Разумеется, это означает, что в процессе его возникновения Земля превратится в пар. Таким образом, кривая предсказывает окончательную участь Земли. Поскольку возраст нашего Солнца средний, т. е. ему примерно 5 млрд лет, пройдет еще 5 млрд лет, прежде чем оно поглотит Землю. (По иронии судьбы, Земля родилась из того же вихревого газового облака, из которого возникло наше Солнце. В настоящее время физики высказывают предположение, что Земля, созданная вместе с Солнцем, воссоединится с ним.)
И наконец, когда будет израсходован гелий, ядерная печь снова прекратит работу, и гравитация уничтожит звезду. Красный гигант сожмется и станет белым карликом — миниатюрной звездой, сократившейся примерно до размеров планеты Земля[112]. Белые карлики светят слабо, так как относятся к нижней части кривой, которой соответствует совсем небольшой избыток энергии согласно формуле E = mc2. Белый карлик сжигает то немногое, что остается на нижней части кривой.
Наше Солнце в конце концов превратится в белого карлика и на протяжении миллиардов лет будет медленно умирать, так как истощит все свои запасы ядерного топлива. В итоге оно станет темной, выгоревшей карликовой звездой. Однако считается, что если звезда обладает достаточной массой (в несколько раз превышающей массу нашего Солнца), то большинство элементов, содержащихся в белом карлике, будут по-прежнему участвовать в реакциях с образованием все более тяжелых элементов и со временем дело дойдет до железа. Излишки массы уже не будут давать энергии, ядерная печь прекратит работу. Гравитация вновь окажется сильнее и будет сжимать звезду, пока температура не увеличится сразу в тысячу раз, достигая триллионов градусов. В этот момент железное ядро сжимается, а наружная оболочка белого карлика разрушается, процесс сопровождается самым мощным в галактике выбросом энергии и образованием взрывающейся звезды — сверхновой. Всего одной сверхновой достаточно, чтобы на время затмить целую галактику со 100 млрд звезд.
После взрыва сверхновой мы обнаруживаем совершенно мертвую звезду — нейтронную звезду размером с Манхэттен. Плотность составляющих нейтронной звезды настолько велика, что, грубо говоря, нейтроны «трутся» друг о друга. Хотя нейтронные звезды почти невидимы, их можно обнаружить с помощью приборов. Вращаясь, они распространяют излучение, так что действуют как космические маяки. Мы видим их как мерцающие звезды, или пульсары. (Этот сценарий выглядит, как научная фантастика, тем не менее свыше 400 пульсаров было обнаружено с тех пор, как их открыли в 1967 г.)
Компьютерные вычисления показали, что большинство элементов, более тяжелых, чем железо, могут синтезироваться при температурах и давлении, характерных для сверхновой звезды. Когда звезда взрывается, в космический вакуум выбрасывается уйма «звездного мусора», состоящего из тяжелых элементов. Этот «мусор» в итоге смешивается с прочими газами, пока не накопится достаточное количество водорода, чтобы процесс гравитационного сжатия начался опять. Из газопылевых облаков, изобилующих тяжелыми элементами, рождаются звезды второго поколения. Некоторые из этих звезд (такие как наше Солнце) окружены планетами, содержащими тяжелые элементы.
Так разрешается давняя загадка космологии. Наши тела состоят из элементов, более тяжелых, чем железо, но наше Солнце не настолько горячее, чтобы создать такие элементы. Если Земля и атомы нашего тела возникли из того самого газового облака, откуда тогда в нашем теле взялись тяжелые элементы? Вывод однозначен: тяжелые элементы нашего тела были синтезированы в сверхновой звезде, которая взорвалась до появления нашего Солнца. Другими словами, некая безымянная сверхновая звезда взорвалась миллиарды лет назад, породив исходное газовое облако, из которого и образовалась наша Солнечная система.
Эволюцию звезды можно представить в виде автомата для игры в пинбол, как на рис. 10.1, имеющего форму кривой энергии связи. Шар начинает движение сверху, перескакивая от водорода к гелию, от более легких элементов к более тяжелым. При каждом его скачке по кривой появляется звезда другого типа. И наконец, шар достигает нижней части кривой, где находится железо, и в результате взрыва рождается сверхновая звезда. Затем звездное вещество опять собирается в новую звезду, богатую водородом, и процесс «игры в пинбол» возобновляется.
Отметим, однако, что существуют два способа движения шара вниз по кривой. Это движение может начаться с другой стороны кривой, с урана, и достигнуть дна единственным скачком, с расщеплением ядра урана. Поскольку средняя масса протонов таких продуктов деления, как цезий и криптон, меньше средней массы протонов урана, избыток массы преобразуется в энергию согласно формуле E = mc2. Это и есть источник энергии атомной бомбы.
Таким образом, кривая энергии связи не только объясняет рождение и смерть звезд и возникновение элементов, но и делает возможным существование водородной и атомной бомб! (Ученых часто спрашивают, можно ли создать ядерные бомбы помимо атомных и водородных. Как видно из кривой энергии связи, ответ на этот вопрос отрицательный. Отметим, что кривая исключает возможность создания кислородной или железной бомбы. Эти элементы расположены вблизи нижней части кривой, поэтому избытка массы не хватит для бомбы.
А упоминающиеся в прессе бомбы вроде нейтронной — это разновидности урановой и водородной бомб.)
Когда впервые слышишь историю жизни звезд, невольно относишься к ней скептически. Ведь никто же не мог прожить 10 млрд лет и стать свидетелем эволюции звезд. Но, поскольку звезд в небе бесчисленное множество, несложно увидеть звезды почти на всех этапах их эволюции. (К примеру, в 1987 г. сверхновая звезда, которую можно было наблюдать невооруженным глазом в южном полушарии, обеспечила нас множеством астрономических данных, соответствующих теоретическим предположениям о схлопывающемся карлике с железным ядром. Кроме того, остаток великолепной сверхновой звезды, которую наблюдали древнекитайские астрономы 4 июля 1054 г., в настоящее время идентицифирован как нейтронная звезда.)
Вдобавок наши компьютерные программы стали настолько точными, что мы в принципе можем численно прогнозировать порядок звездной эволюции. Когда-то у меня был сосед-аспирант, специализировавшийся на астрономии. Он неизменно уходил рано утром и возвращался поздно вечером. Перед уходом говорил, что ставит звезду в духовку, чтобы увидеть, как она растет. Поначалу я думал, что он шутит. Но, когда я стал расспрашивать его, он со всей серьезностью объяснил, что закладывает звезду в компьютер и весь день наблюдает за тем, как она эволюционирует. Поскольку уравнения термодинамики и термоядерных реакций хорошо известны, остается лишь задать определенную массу водорода и дождаться, когда компьютер представит эволюцию этого газа в численном виде. Таким способом можно убедиться, что наша теория звездной эволюции воспроизводит известные стадии жизни звезды, которые мы видим в телескопы.
Черные дыры
Если звезда в 10–50 раз превосходит размерами наше Солнце, тогда гравитация будет продолжать сжимать ее даже после превращения в нейтронную звезду. В отсутствие силы термоядерных реакций, противостоящей силе притяжения, ничто не может помешать окончательному схлопыванию звезды. В этот момент она становится пресловутой черной дырой.
Существование черных дыр в некотором смысле неизбежно. Как мы помним, звезда — это продукт взаимодействия двух космических сил: гравитации, которая стремится сжать звезду, и силы ядерных реакций, которая стремится взорвать звезду, как водородную бомбу. Все этапы истории существования звезды — следствие этого шаткого равновесия между гравитацией и ядерным взаимодействием. Рано или поздно, когда все ядерное топливо гигантской звезды наконец израсходуется и звезда превратится в скопление одних нейтронов, ничто, насколько нам известно, не сможет помешать воздействию мощной силы гравитации. В конце концов гравитация возобладает и уничтожит нейтронную звезду. Звезда завершила свой путь: она родилась, когда гравитация только начала сжимать газообразный водород в небе, создавая звезду, и умерла, когда ядерное топливо кончилось и гравитация вызвала схлопывание звезды.
Плотность черной дыры настолько велика, что свет, подобно ракете, запущенной с Земли, вынужден двигаться по ее орбите. Поскольку свет не в состоянии избежать воздействия гравитационного поля огромной мощности, схлопнувшаяся звезда по цвету становится черной. Так и принято давать определение черным дырам: это сколлапсировавшая звезда, от которой не может исходить свет.
Надо заметить, что у всех небесных тел есть так называемая скорость убегания. Это скорость, необходимая для полного преодоления гравитационного притяжения конкретного тела. К примеру, космический зонд должен развить скорость убегания 25 000 миль в час (40 000 км/ч), чтобы преодолеть гравитационное притяжение Земли и улететь в дальний космос. Такие космические зонды, как «Вояджер», который вышел в открытый космос и покинул Солнечную систему (увозя послание доброй воли к инопланетянам, которым он может повстречаться), развил скорость убегания нашего Солнца. (Мы дышим кислородом, так как атомам кислорода недостает скорости, чтобы преодолеть поле притяжения Земли. Оболочка Юпитера и других газовых гигантов состоит преимущественно из водорода, поскольку их скорость убегания достаточно велика, чтобы удержать изначальный водород ранней Солнечной системы. Таким образом, скорость убегания помогает объяснить эволюцию планет Солнечной системы за последние 5 млрд лет.)
В сущности, ньютонова теория гравитации дает точное соотношение между скоростью убегания и массой звезды. Чем тяжелее планета или звезда и чем меньше ее радиус, тем большая скорость убегания понадобится, чтобы преодолеть силу ее гравитационного притяжения. Еще в 1783 г. английский астроном Джон Мичелл воспользовался этими вычислениями, чтобы предположить, что супермассивная звезда может иметь скорость убегания, равную скорости света. Свет, излучаемый такой массивной звездой, не отдаляется от нее, а движется вокруг по орбите. Таким образом, стороннему наблюдателю эта звезда может показаться совершенно черной. Пользуясь всеми знаниями, имевшимися в XVIII в., Мичелл действительно вычислил массу такой черной дыры[113]. Увы, его теорию сочли бредовой и вскоре забыли. Тем не менее сегодня мы склонны считать, что черные дыры существуют, так как благодаря телескопам и другим приборам увидели в небе белых карликов и нейтронные звезды.
Объяснить, почему черные дыры черные, можно двумя способами. С точки зрения прохожего, сила, действующая между звездой и лучом света, настолько велика, что его траектория изогнута и представляет собой окружность. Можно также принять точку зрения Эйнштейна, согласно которой «кратчайшее расстояние между двумя точками — кривая». Искривление луча света до полной окружности означает, что и само пространство свернуто в круг. Такое возможно лишь в том случае, если черная дыра полностью сжала участок пространства-времени вокруг нее, поэтому луч света перемещается в гиперсфере. Этот участок пространства-времени теперь отделен от окружающего пространства-времени, а само пространство «разорвано».
Мост Эйнштейна-Розена
Релятивистское описание черных дыр фигурирует в работе Карла Шварцшильда. В 1916 г., всего через несколько месяцев после того, как Эйнштейн записал свои знаменитые уравнения, Шварцшильд сумел найти для них точное решение и вычислить гравитационное поле массивной стационарной: звезды.
Решение Шварцшильда имело несколько интересных особенностей. Во-первых, вокруг черной дыры находится «точка невозврата». Любой объект, приблизившийся на расстояние, меньшее, чем этот радиус, неизбежно затянет в черную дыру, спастись ему не удастся. Человек, которому не посчастливится оказаться в пределах радиуса Шварцшильда, будет захвачен черной дырой и раздавлен насмерть. В настоящее время это расстояние от черной дыры называется радиусом Шварцшильда, или горизонтом событий (самой удаленной видимой точкой).
Во-вторых, каждый, кто окажется в пределах радиуса Шварцшильда, обнаружит «зеркальную вселенную» по «другую сторону» пространства-времени (рис. 10.2). Эйнштейна не беспокоило существование этой причудливой зеркальной Вселенной, потому что сообщение с ней было невозможным. Любой космический зонд, отправленный в центр черной дыры, столкнется с бесконечной искривленностью; иначе говоря, гравитационное поле окажется бесконечным, а любой материальный объект будет уничтожен. Электроны оторвутся от атомов, и даже протоны и нейтроны в ядре разнесет в разные стороны. Кроме того, чтобы проникнуть в другую вселенную, зонду понадобится лететь со скоростью, превышающей скорость света, а это невозможно. Таким образом, хотя зеркальная Вселенная математически необходима для понимания решения Шварцшильда, наблюдать ее физически не удастся никогда.
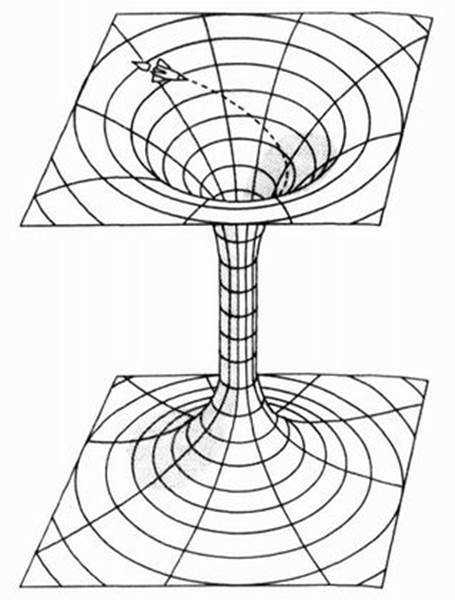
Рис. 10.2. Мост Эйнштейна-Розена соединяет две разных вселенных. Эйнштейн считал, что любая ракета, очутившаяся на этом мосту, будет уничтожена, значит, сообщение между этими двумя вселенными невозможно. Но более поздние вычисления показали, что путешествия помосту хоть и чрезвычайно трудны, но все-таки возможны.
В итоге известный мост Эйнштейна-Розена, соединяющий две вселенных (мост назван в честь Эйнштейна и его соавтора Натана Розена), считается математической причудой. Этот мост необходим для получения математически последовательной теории черных дыр, однако по мосту Эйнштейна-Розена попасть в зеркальную вселенную невозможно. Мосты Эйнштейна-Розена вскоре обнаружились и в других решениях гравитационных уравнений, таких, как решение Райснера-Нордстрёма для черной дыры с электрическим зарядом… Тем не менее мост Эйнштейна-Розена оставался любопытным, но забытым приложением к теории относительности.
Ситуация начала меняться с появлением труда новозеландского математика Роя Керра, который в 1963 г. нашел еще одно точное решение уравнений Эйнштейна. Керр полагал, что любая коллапсирующая звезда вращается. Как вращающийся фигурист, скорость которого возрастает, когда он прижимает к себе руки, звезда неизбежно будет вращаться быстрее по мере схлопывания. Таким образом, стационарное решение Шварцшильда для черных дыр не было самым физически релевантным решением уравнений Эйнштейна.
Предложенное Керром решение стало сенсацией в вопросах относительности. Астрофизик Субраманьян Чандрасекар однажды сказал:
Самым ошеломляющим событием за всю мою научную жизнь, т. е. более чем за сорок пять лет, стало осознание, что точное решение уравнений общей теории относительности Эйнштейна, открытое новозеландским математиком Роем Керром, дает абсолютно точное отображение бессчетного множества массивных черных дыр, наполняющих вселенную. Этот «трепет перед прекрасным», этот невероятный факт, что открытие, к которому привел поиск красоты в математике, обнаружило ее точную копию в Природе, убеждают меня, что красота — то, на что человеческий разум отзывается на самом глубинном, содержательном уровне[114].
Однако Керр обнаружил, что массивная вращающаяся звезда не сжимается в точку. Вместо этого вращающаяся звезда сплющивается, пока в конце концов не превращается в кольцо, обладающее примечательными свойствами. Если запустить зонд в черную дыру сбоку, он ударится об это кольцо и будет полностью уничтожен. Искривленность пространства-времени остается бесконечной, если приближаться к кольцу сбоку. Если можно так выразиться, центр все так же окружен «кольцом смерти». Но, если запустить космический зонд в кольцо сверху или снизу, ему придется иметь дело с большой, но конечной искривленностью; иначе говоря, гравитационная сила не будет бесконечной.
Этот весьма неожиданный вывод из решения Керра означает, что любой космический зонд, запущенный во вращающуюся черную дыру вдоль оси ее вращения, может в принципе пережить огромное, но конечное воздействие гравитационных полей в центре и проделать весь путь до зеркальной Вселенной, избежав гибели под воздействием бесконечной искривленности. Мост Эйнштейна-Розена действует как туннель, соединяющий две области пространства-времени; это и есть «червоточина», или «кротовина». Таким образом, черная дыра Керра — ворота в другую вселенную.
А теперь представим, что наша ракета очутилась на мосту Эйнштейна-Розена. Приближаясь к вращающейся черной дыре, она видит кольцеобразную вращающуюся звезду. Поначалу кажется, что ракету, спускающуюся навстречу черной дыре со стороны северного полюса, ждет катастрофическое столкновение. Но по мере приближения к кольцу свет зеркальной Вселенной достигает наших датчиков. Поскольку все электромагнитное излучение, в том числе и от радаров, движется по орбите черной дыры, на экранах наших радаров появляются сигналы, многократно проходящие вокруг черной дыры. Создается эффект, напоминающий зеркальную «комнату смеха», где нас вводят в заблуждение многочисленные отражения со всех сторон. Свет отражается рикошетом от множества зеркал, создавая иллюзию, будто комната полна наших точных копий.
Тот же самый эффект наблюдается при прохождении сквозь черную дыру согласно Керру. Поскольку один и тот же луч света обходит черную дыру по орбите множество раз, радар в нашей ракете обнаруживает изображения, вращающиеся вокруг черной дыры и создающие иллюзию объектов, которых на самом деле там нет.
Варп-скорость 5
Означает ли это, что с помощью черных дыр можно путешествовать по всей галактике, как в «Звездном пути» и других научно-фантастических фильмах?
Как мы видели ранее, искривленность конкретного пространства обусловлена количеством материи-энергии, содержащейся в этом пространстве (принцип Маха). Знаменитая формула Эйнштейна дает нам точную степень искривления пространства-времени, вызванного наличием материи-энергии.
Когда мы вместе с капитаном Кирком устремляемся сквозь гиперпространство с «варп-скоростью 5», «кристаллы дилития», приводящие в движение «Энтерпрайз», должны творить чудеса, деформируя пространство и время. Это означает, что кристаллы дилития обладают магической способностью сворачивать пространственно-временной континуум в крендель, т. е. являются вместилищами неисчерпаемых запасов материи и энергии.
Если «Энтерпрайз» совершает рейс с Земли на ближайшую звезду, он не перемещается физически к альфе Центавра — скорее, альфа Центавра приближается к «Энтерпрайзу». Представьте себе, что вы сидите на ковре и накидываете лассо на стол, находящийся на расстоянии нескольких метров. Если вы достаточно сильны, а пол сравнительно гладкий, можно тянуть лассо, пока ковер под вами не соберется в складки. Если потянуть как следует, стол подъедет к вам, «расстояние» между столом и вами исчезнет в складках ковра. Тогда можно просто перепрыгнуть через этот «ковровый варп». Иными словами, вы почти не двигались, а пространство между вами и столом сократилось, и вы просто перешагнули сжавшееся расстояние. Так и «Энтерпрайз» на самом деле вовсе не преодолевает все пространство, отделяющее его от альфы Центавра: он просто перемещается через деформированное пространство-время — «червоточину». Для того чтобы лучше понять, что происходит, когда спускаешься по мосту Эйнштейна-Розена, поговорим о топологии «червоточин».
Для того чтобы представить себе многосвязные пространства, вообразите, что вы шагаете солнечным днем по Пятой авеню в Нью-Йорке, размышляете о своих делах, и вдруг прямо перед вами открывается странное парящее в воздухе окно, очень похожее на зеркало Алисы. (На время забудем, что энергия, которая потребуется для открывания такого окна, способна разрушить Землю. Это чисто гипотетический пример.)
Вы приближаетесь к зависшему над землей окну, чтобы получше рассмотреть его, и в ужасе обнаруживаете прямо перед собой голову злобного с виду тираннозавра реке. Вы уже готовы спасаться бегством, как вдруг замечаете, что у тираннозавра нет туловища. Он не причинит вам никакого вреда, потому что его тело находится по другую сторону окна. Когда вы заглядываете за окно, чтобы осмотреть туловище динозавра, то видите только улицу, как будто ни динозавра, ни окна нет вообще. Озадачившись, вы медленно обходите окно и с облегчением убеждаетесь, что тираннозавра нигде нет. Но заглянув в окно с обратной стороны, вы видите прямо перед собой голову бронтозавра (рис. 10.3)!
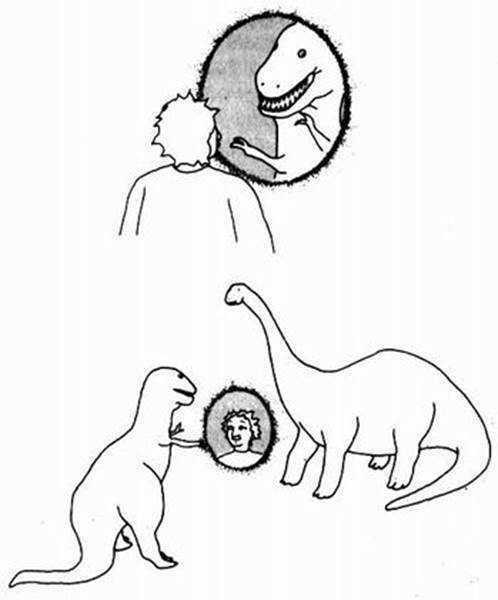
Рис. 10.3. В этом чисто гипотетическом примере в нашей Вселенной открывается «окно», или «червоточина». Заглянув в окно с одной стороны, мы видим одного динозавра. Заглянув с другой стороны, видим второго динозавра. Из другой Вселенной видно, что окно открылось между двумя динозаврами. В окне динозавры видят странное маленькое существо — человека.
Перепугавшись, вы снова обходите вокруг окна, попутно взглянув на него сбоку. К вашему изумлению, окно вместе с тираннозавром и бронтозавром исчезает бесследно. Вы еще несколько раз обходите вокруг повисшего в воздухе окна. С одной стороны, видите голову тираннозавра, с другой — голову бронтозавра. А когда смотрите сбоку, то и зеркало, и динозавры исчезают.
Что происходит?
В некой далекой Вселенной тираннозавр и бронтозавр сошлись, чтобы драться не на жизнь, а на смерть. Когда они стояли один напротив другого, между ними вдруг возникло парящее в воздухе окно. Заглянув в это окно, тираннозавр неожиданно для себя увидел голову тщедушного, тощего млекопитающего с растрепанными волосами и крошечным лицом — человека. Голова видна отчетливо, а тела нет. Когда в то же самое окно заглянул бронтозавр, то увидел Пятую авеню с ее магазинами и транспортом. Потом тираннозавр заметил, что человек в окне исчез, только чтобы появиться по другую сторону окна и показаться бронтозавру.
А теперь представьте, что внезапный порыв ветра унес вашу шляпу в окно. Вы видите, как шляпа летит по воздуху в другой Вселенной, но нигде на Пятой авеню ее нет. Тяжело вздохнув, вы отчаянным движением суете руку в окно, чтобы поймать шляпу. Тираннозавр при этом видит, как шляпа вылетает из окна и скрывается из виду. Потом он видит, как из окна высовывается отделенная от тела рука, тщетно пытающаяся ухватить шляпу.
Ветер вдруг меняет направление, и шляпа летит в другую сторону. Вы просовываете в окно вторую руку, но уже с другой стороны. И попадаете в неловкое положение: обе ваши руки засунуты в окно, но с разных сторон. Вы не видите собственных пальцев, вам кажется, что обе руки исчезли.
Что при этом видят динозавры? Они видят две судорожно машущие крошечные ручонки, высунувшиеся из окна с обеих сторон. А остального тела нет (рис. 10.4).
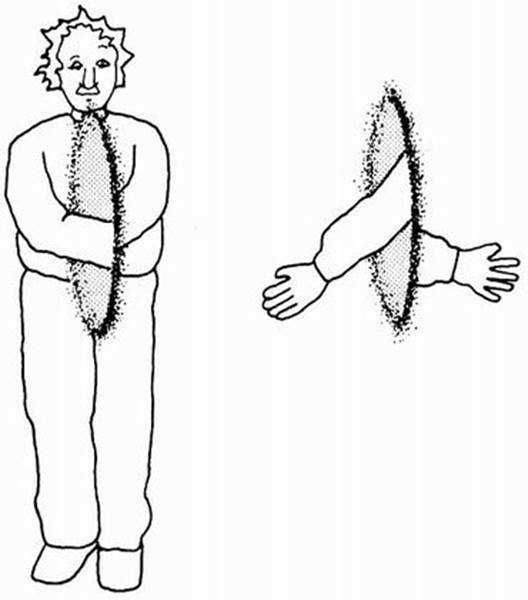
Рис. 10.4. Если мы засунем в окно наши руки с разных сторон, будет казаться, что они исчезли. Туловище есть, а рук нет. В другой Вселенной по обеим сторонам окна появятся обе руки, но они не будут соединены с телом.
Этот пример демонстрирует лишь некоторые из удивительных искажений пространства и времени, которые можно придумать с помощью многосвязных пространств.
megaobuchalka.ru
Черные дыры и структура пространства-времени. 2. Черные дыры и квантовая механика
Хуан Малдасена (Juan Maldacena),
Институт высших исследований, Школа естественных наук, Принстон, Нью-Джерси, США
Английский оригинал Видеозапись Презентация лекции (pdf, 656 Кб)
2. Черные дыры и квантовая механика
Следующий сюрприз ждал ученых, когда они занялись изучением квантовых эффектов. В квантовой механике вакуум — это не просто полное отсутствие элементарных частиц. Вакуум — это весьма интересное состояние пространства, в котором постоянно возникают и тут же аннигилируют пары «частица-античастица». В спрямленном пространстве чистого выхода в виде возникших из вакуума частиц мы не имеем в силу закона сохранения энергии. То есть, фактически, частицы взаимно аннигилируются, даже не успев родиться. В 1974 году всё тот же Стивен Хокинг доказал, что вблизи горизонта это не так. Имеется ненулевая вероятность рождения пары частиц, сразу же оказывающихся по разные стороны бесконечно тонкого горизонта, причем закон сохранения энергии не нарушается, поскольку частица снаружи горизонта обладает, с точки зрения стороннего наблюдателя, положительной энергией, а частица внутри горизонта — отрицательной (при этом с точки зрения наблюдателя внутри сферы Шварцшильда всё выглядит с точностью до наоборот). Тепловое распределение испускаемых частиц соответствует температуре, которая обратно пропорциональна массе черной дыры. Даже для черных дыр звездной массы эта температура настолько близка к абсолютному нулю, что этот эффект зарегистрировать фактически невозможно. Однако, если черная дыра достаточно долго пробыла бы в полном вакууме, то за счёт эффекта Хокинга она постепенно бы теряла массу через излучение рождающихся на поверхности частиц. Теряя массу, черная дыра разогревается. Черная дыра с массой порядка 1019 кг (масса большого горного хребта) разогреется до температуры в несколько тысяч градусов и будет вылядеть белой. Однако мощность такого излучения будет составлять не больше милливатта, и зарегистрировать его по-прежнему практически невозможно. Но, чем меньше становится масса изолированной черной дыры, тем выше становится её температура, и тем быстрее она «испаряется», пока, вероятно, не испарится полностью. Фактически, если бы нам удалось сжать до плотности черной дыры всего несколько килограммов вещества (на практике нам этого, конечно, не дано!), такая черная дыра испарилась бы меньше, чем за одну миллисекунду, а энергии при этом выделилось бы больше, чем при взрыве водородной бомбы.
Наличие такого теплового излучения у черных дыр сразу создает две головоломки: 1) причины повышения энтропии черной дыры и 2) информационный парадокс. Попробую объяснить их смысл подробнее.
2.1. Энтропия черных дыр
В классической физике тепловые свойства вещества обусловлены движением составляющих его материальных частиц. Например, температура воздуха связана со среднеквадратичной скоростью теплового движения его молекул. Родственное температуре понятие называется энтропия. Энтропия дает количественное выражение степени хаотичности движения составляющих системы. Законы термодинамики позволяют связать энтропию с температурой, массой и объемом, благодаря чему её можно рассчитать, не зная микроскопических деталей строения системы. Хокинг и Бекенштейн (Bekenstein) показали, что энтропия черной дыры пропорциональна площади её горизонта, деленной на квадрат т. н. гравитационной длины Планка lPlanck = 10–33 см. Для черной дыры макроскопических размеров значение энтропии получается просто чудовищным. Однако законов термодинамики в данном случае, похоже, ничто не отменяет, и они продолжают действовать даже с учетом, по сути, бесконечного «вклада» невидимых недр черной дыры в её энтропию. Результаты эти крайне озадачивают, прежде всего, потому, что совершенно не ясно, из чего «складывается» энтропия черной дыры, поскольку никаких явных компонентов, которые своим хаотичным движением могли бы способствовать беспредельному увеличению энтропии, внутри черной дыры нет. По крайней мере, мы не можем усмотреть их «снаружи», поскольку нам видится только по-настоящему «черная» дыра — бездонный провал в ткани пространства-времени, и чтобы понять, из каких «компонентов» она реально состоит, необходимо найти какие-то самые фундаментальные составные элементы, на которые можно разложить саму геометрию пространства-времени.
Крайне интересно еще и то, что энтропия черной дыры пропорциональна её площади (квадрату радиуса), а не объему (кубу радиуса). В начале 1990-х годов Хофт (‘t Hooft) и Зюскинд (Susskind) предположили, что в теории, объединяющей квантовую механику и гравитацию, число элементарных компонентов, необходимых для исчерпывающего описания системы, пропорционально площади окружающей поверхности, в которую она заключена. А это означает, что структура пространства-времени в корне отличается от структуры твёрдого тела, в котором число таких элементарных компонентов (материальных точек или атомов) возрастает пропорционально её объему, а отнюдь не площади. С практической точки зрения такое ограничение энтропии поверхностью сферы не кажется чересчур принципиальным, однако, с теоретической точки зрения, оно приводит к коренному изменению представлений о мире, поскольку оказывается возможным описать замкнутую пространственно-временную область исключительно по поведению компонентов, расположенных на её внешней границе.
2.2. Информационный парадокс
Мы уже отмечали, что происхождение чёрной дыры может быть различным, однако свойства самой дыры от этого не меняются. Обычно в физике при фазовом переходе или ином преобразовании от исходного состояния вещества зависит и конечное состояние вещества. Иногда различия едва заметны, но они присутствуют. Позвольте привести пример. Возьмём две абсолютно одинаковые тарелки, напишем на одной из них букву А, а на другой — букву Б, после чего разобьём ту и другую на мелкие кусочки. На первый взгляд результат идентичен — две груды мелких осколков на полу. Однако, тщательно изучив обе кучи битого фарфора, мы рано или поздно сумеем разобраться, на какой из исходных тарелок какая буква значилась.
А теперь предположим, что одну из этих тарелок мы бросили в чёрную дыру. Судя по всему, что мы знаем на сегодняшний день, рано или поздно всё вещество этой черной дыры вместе с остатками тарелки испарится в виде излучения Хокинга. Согласно теории Хокинга это будет чисто тепловое излучение, не зависящее от исходного состояния ни самой черной дыры, ни, тем более, попавшей в неё тарелки. То есть, мы, судя по всему, никогда не восстановим информацию о том, какая буква была изначально написана на тарелке.
На первый взгляд это кажется чистой воды академической казуистикой. Мы же постоянно что-то забываем в обычной жизни, и нам это не кажется противоестественным! Однако проблема-то на самом деле крайне серьезна, поскольку квантовая механика утверждает, что законы, управляющие этим процессом, таковы, что подобная информация должна быть в принципе восстановима. Поэтому решение проблемы сохранения информации является необходимостью с точки зрения построения последовательной и внутренне непротиворечивой квантовой теории гравитации. Информационный парадокс обязан быть разрешен в рамках такой теории.
Многие видные физики, включая С. Хокинга, полагали, что это невозможно. Они считали, что всякая информация внутри черной дыры уничтожается бесследно, и, как следствие, предлагали отказаться и от идеи Великого объединения теории взаимодействий в рамках квантово-механических представлений, и от квантовой механики, как таковой, поскольку она постулирует невыполнимый принцип сохранения информации.
Однако дальнейшее осмысление этого вопроса привело к интересным последствиям, а именно, к развитию теории струн в физике элементарных частиц.
elementy.ru
Черные дыры в пространстве и времени
Черные дыры - это порождение гигантских сил тяготения. Они возникают, когда в ходе сильного сжатия большей массы материи возрастающее гравитационное поле ее становится настолько сильным, что не выпускает даже свет, из черной дыры не может вообще ничто выходить. В нее можно только упасть под действием огромных сил тяготения, но выхода оттуда нет.
С какой силой притягивает центральная масса какое-либо тело, находящееся на ее поверхности? Если радиус массы велик, то ответ совпадал с классическим законом Ньютона. Но когда принималось, что та же масса сжата до все меньшего и меньшего радиуса, постепенно проявлялись отклонения от закона Ньютона — сила притяжения получалась пусть незначительно, но несколько большей. При совершенно фантастических же сжатиях отклонения были заметнее. Но самое интересное, что для каждой массы существует свой определенный радиус, при сжатии до которого сила тяготения стремилась к бесконечности! Такой радиус в теории был назван гравитационным радиусом. Гравитационный радиус тем больше, чем больше масса тела. Но даже для астрономических масс он очень мал: для массы Земли это всего один сантиметр.
В 1939 году американские физики Р.Оппенгеймер и Х.Снайдер дали точное математическое описание того, что будет происходить с массой, сжимающейся под действием собственного тяготения до все меньших размеров. Если сферическая масса, уменьшаясь, сожмется до размеров, равных или меньших, чем гравитационный радиус, то потом никакое внутреннее давление вещества, никакие внешние силы не смогут остановить дальнейшее сжатие. Действительно, ведь если бы при размерах, равных гравитационному радиусу, сжатие остановилось бы, то силы тяготения на поверхности массы были бы бесконечно велики и ничто с ними не могло бы бороться, они тут же заставят массу сжиматься дальше. Но при стремительном сжатии — падении вещества к центру — силы тяготения не чувствуются.
Всем известно, что при свободном падении наступает состояние невесомости и любое тело, не встречая опоры, теряет вес. То же происходит и со сжимающейся массой: на ее поверхности сила тяготения — вес — не ощущается. После достижения размеров гравитационного радиуса остановить сжатие массы нельзя. Она неудержимо стремится к центру. Такой процесс физики называют гравитационным коллапсом, а результатом является возникновение черной дыры. Именно внутри сферы с радиусом, равным гравитационному, тяготение столь велико, что не выпускает даже свет. Эту область Дж.Уиллер назвал в 1968 году черной дырой.
Название оказалось крайне удачным и было моментально подхвачено всеми специалистами. Границу черной дыры называют горизонтом событий. Название это понятно, ибо из-под этой границы не выходят к внешнему наблюдателю никакие сигналы, которые могли бы сообщить сведения о происходящих внутри событиях. О том, что происходит внутри черной дыры, внешний наблюдатель никогда ничего не узнает.
Итак, вблизи черной дыры необычно велики силы тяготения, но это еще не все. В сильном поле тяготения меняются геометрические свойства пространства и замедляется течение времени.
Около горизонта событий кривизна пространства становится очень сильной. Чтобы представить себе характер этого искривления, поступим следующим образом. Заменим в наших рассуждениях трехмерное пространство двумерной плоскостью (третье измерение уберем) — нам будет легче изобразить ее искривление. Пустое пространство изображается плоскостью. Если мы теперь поместим в это пространство тяготеющий шар, то вокруг него пространство слегка искривится - прогнется. Представим себе, что шар сжимается и его поле тяготения увеличивается. Перпендикулярно пространству отложена координата времени, как его измеряет наблюдатель на поверхности шара. С ростом тяготения увеличивается искривление пространства. Наконец, возникает черная дыра, когда поверхность шара сожмется до размеров, меньше горизонта событий, и «прогиб» пространства сделает стенки в прогибе вертикальными. Ясно, что вблизи черной дыры на столь искривленной поверхности геометрия будет совсем не похожа на евклидову геометрию на плоскости. С точки зрения геометрии пространства черная дыра действительно напоминает дыру в пространстве.
Обратимся теперь к темпу течения времени. Чем ближе к горизонту событий, тем медленнее течет время с точки зрения внешнего наблюдателя. На границе черной дыры его бег и вовсе замирает. Такую ситуацию можно сравнить с течением воды у берега реки, где ток воды замирает. Это образное сравнение принадлежит немецкому профессору Д.Либшеру.
Но совсем иная картина представляется наблюдателю, который в космическом корабле отправляется в черную дыру. Огромное поле тяготения на ее границе разгоняет падающий корабль до скорости, равной скорости света. И тем не менее далекому наблюдателю кажется, что падение корабля затормаживается и полностью замирает на границе черной дыры. Ведь здесь, с его точки зрения, замирает само время.
С приближением скорости падения к скорости света время на корабле также замедляет свой бег, как и на любом быстро летящем теле. И вот это замедление побуждает замирание падения корабля. Растягивающаяся до бесконечности картина приближения корабля к границе черной дыры из-за все большего и большего растягивания секунд на падающем корабле измеряется конечным числом этих все удлиняющихся (с точки зрения внешнего наблюдателя) секунд. По часам падающего наблюдателя или по его пульсу до пересечения границы черной дыры протекло вполне конечное число секунд. Бесконечно долгое падение корабля по часам далекого наблюдателя уместилось в очень короткое время падающего наблюдателя. Бесконечное для одного стало конечным для другого.
Вот уж поистине фантастическое изменение представлений о течении времени. То, что мы говорили о наблюдателе на космическом корабле, относится и к воображаемому наблюдателю на поверхности сжимающего шара, когда обрадуется черная дыра.
Наблюдатель, упавший в черную дыру, никогда не сможет оттуда выбраться, как бы ни были мощны двигатели его корабля. Он не сможет послать оттуда и никаких сигналов, никаких сообщений. Ведь даже свет — самый быстрый вестник в природе — оттуда не выходит. Для внешнего наблюдателя само падение корабля растягивается по его часам до бесконечности. Значит, то, что будет происходить с падающим наблюдателем и его кораблем внутри черной дыры, протекает уже вне времени внешнего наблюдателя (после его бесконечности по времени). В этом смысле черные дыры представляют собой «дыры во времени Вселенной».
Конечно, сразу оговоримся, что это вовсе не означает, что внутри черной дыры время не течет. Там время течет, но это другое время, текущее иначе, чем время внешнего наблюдателя. Что же произойдет с наблюдателем, если он отважится отправиться в черную дыру на космическом корабле? Силы тяготения будут увлекать его в область, где эти силы все сильнее и сильнее. Если в начале падения в корабле наблюдатель находился в невесомости и ничего неприятного не испытывал, то в ходе падения ситуация изменится. Чтобы понять, что произойдет, вспомним про приливные силы тяготения. Их действие связано с тем, что точки тела, находящиеся ближе к центру тяготения, притягиваются сильнее чем расположенные дальше. В результате притягиваемое тело растягивается. В начале падения наблюдателя в черную дыру приливное растяжение может быть ничтожным. Но оно неизбежно нарастает в ходе падения.
Как показывает теория, любое падающее в черную дыру тело попадает в область, где приливные силы становятся бесконечными. Это так называемая сингулярность внутри черной дыры. Здесь любое тело или частица будут разорваны приливными силами и перестанут существовать. Пройти сквозь сингулярность и не разрушиться не может ничто. Но если такой исход совершенно неизбежен для любых тел внутри черной дыры, то это означает, что в сингулярности перестает существовать и время. Свойства времени зависят от протекающих процессов. Теория утверждает, что в сингулярности свойства времени изменяются настолько сильно, что его непрерывный поток обрывается, оно распадается на кванты. Здесь надо еще раз вспомнить, что теория относительности показала необходимость рассматривать время и пространство совместно, как единое многообразие. Поэтому правильнее говорить о распаде в сингулярности на кванты единого пространства-времени.
Современная наука раскрыла связь времени с физическими процессами, позвонило «прощупать» первые звенья цепи времени в прошлом и проследить за ее свойствами в далеком будущем.
biofile.ru
Чёрная дыра — WiKi
Компьютерная симуляция слияния двух чёрных дыр, от которого впервые были зарегистрированы гравитационные волныЧёрная дыра́ — область пространства-времени[1], гравитационное притяжение которой настолько велико, что покинуть её не могут даже объекты, движущиеся со скоростью света, в том числе кванты самого света. Граница этой области называется горизонтом событий, а её характерный размер — гравитационным радиусом. В простейшем случае сферически симметричной чёрной дыры он равен радиусу Шварцшильда.
Теоретически возможность существования таких областей пространства-времени следует из некоторых точных решений уравнений Эйнштейна, первое[2] из которых было получено Карлом Шварцшильдом в 1915 году. Точный изобретатель термина неизвестен[3], но само обозначение было популяризовано Джоном Арчибальдом Уилером и впервые публично употреблено в популярной лекции «Наша Вселенная: известное и неизвестное» (англ. Our Universe: the Known and Unknown) 29 декабря 1967 года[Комм 1]. Ранее подобные астрофизические объекты называли «сколлапсировавшие звёзды» или «коллапсары» (от англ. collapsed stars), а также «застывшие звёзды» (англ. frozen stars)[4].
Вопрос о реальном существовании чёрных дыр тесно связан с тем, насколько верна теория гравитации, из которой следует их существование. В современной физике стандартной теорией гравитации, лучше всего подтверждённой экспериментально, является общая теория относительности (ОТО), уверенно предсказывающая возможность образования чёрных дыр (но их существование возможно и в рамках других (не всех) моделей, см. Альтернативные теории гравитации). Поэтому наблюдаемые данные анализируются и интерпретируются, прежде всего, в контексте ОТО, хотя, строго говоря, эта теория пока не является интенсивно экспериментально протестированной для условий, соответствующих области пространства-времени в непосредственной близости от горизонта чёрных дыр звёздных масс (однако хорошо подтверждена в условиях, соответствующих сверхмассивным чёрным дырам[5], и с точностью до 94 % согласуется с первым гравитационно-волновым сигналом). Поэтому утверждения о непосредственных доказательствах существования чёрных дыр, в том числе и в этой статье ниже, строго говоря, следует понимать в смысле подтверждения существования астрономических объектов, таких плотных и массивных, а также обладающих некоторыми другими наблюдаемыми свойствами, что их можно интерпретировать как чёрные дыры общей теории относительности[5].
Кроме того, чёрными дырами часто называют объекты, не строго соответствующие данному выше определению, а лишь приближающиеся по своим свойствам к такой чёрной дыре — например, это могут быть коллапсирующие звёзды на поздних стадиях коллапса. В современной астрофизике этому различию не придаётся большого значения[6], так как наблюдаемые проявления «почти сколлапсировавшей» («замороженной») звезды и «настоящей» («извечной») чёрной дыры практически одинаковы. Это происходит потому, что отличия физических полей вокруг коллапсара от таковых для «извечной» чёрной дыры уменьшаются по степенным законам с характерным временем порядка гравитационного радиуса, делённого на скорость света — то есть за доли секунды для чёрных дыр звёздных масс и часы для сверхмассивных чёрных дыр[7].
Различают четыре сценария образования чёрных дыр:
- два реалистичных
- и два гипотетических
Предыстория
«Чёрная звезда» Мичелла (1784—1796)
«Чёрная дыра» Мичелла
Концепция массивного тела, гравитационное притяжение которого настолько велико, что скорость, необходимая для преодоления этого притяжения (вторая космическая скорость), равна или превышает скорость света, впервые была высказана в 1784 году Джоном Мичеллом в письме[8], которое он послал в Королевское общество. Письмо содержало расчёт, из которого следовало, что для тела с радиусом в 500 солнечных радиусов и с плотностью Солнца вторая космическая скорость на его поверхности будет равна скорости света[9]. Таким образом, свет не сможет покинуть это тело, и оно будет невидимым[10]. Мичелл предположил, что в космосе может существовать множество таких недоступных наблюдению объектов. В 1796 году Лаплас включил обсуждение этой идеи в свой труд «Exposition du Systeme du Monde», однако в последующих изданиях этот раздел был опущен. Тем не менее, именно благодаря Лапласу эта мысль получила некоторую известность[10].
От Мичелла до Шварцшильда (1796—1915)
На протяжении XIX века идея тел, невидимых вследствие своей массивности, не вызывала большого интереса у учёных. Это было связано с тем, что в рамках классической физики скорость света не имеет фундаментального значения. Однако в конце XIX — начале XX века было установлено, что сформулированные Дж. Максвеллом законы электродинамики, с одной стороны, выполняются во всех инерциальных системах отсчёта, а с другой стороны, не обладают инвариантностью относительно преобразований Галилея. Это означало, что сложившиеся в физике представления о характере перехода от одной инерциальной системы отсчёта к другой нуждаются в значительной корректировке.
В ходе дальнейшей разработки электродинамики Г. Лоренцем была предложена новая система преобразований пространственно-временных координат (известных сегодня как преобразования Лоренца), относительно которых уравнения Максвелла оставались инвариантными. Развивая идеи Лоренца, А. Пуанкаре предположил, что все прочие физические законы также инвариантны относительно этих преобразований.
В 1905 году А. Эйнштейн использовал концепции Лоренца и Пуанкаре в своей специальной теории относительности (СТО), в которой роль закона преобразования инерциальных систем отсчёта окончательно перешла от преобразований Галилея к преобразованиям Лоренца. Классическая (галилеевски-инвариантная) механика была при этом заменена на новую, Лоренц-инвариантную релятивистскую механику. В рамках последней скорость света оказалась предельной скоростью, которую может развить физическое тело, что радикально изменило значение чёрных дыр в теоретической физике.
Однако ньютоновская теория тяготения (на которой базировалась первоначальная теория чёрных дыр) не является лоренц-инвариантной. Поэтому она не может быть применена к телам, движущимся с околосветовыми и световой скоростями. Лишённая этого недостатка релятивистская теория тяготения была создана, в основном, Эйнштейном (сформулировавшим её окончательно к концу 1915 года) и получила название общей теории относительности (ОТО)[10]. Именно на ней и основывается современная теория астрофизических чёрных дыр[6].
По своему характеру ОТО является геометрической теорией. Она предполагает, что гравитационное поле представляет собой проявление искривления пространства-времени (которое, таким образом, оказывается псевдоримановым, а не псевдоевклидовым, как в специальной теории относительности). Связь искривления пространства-времени с характером распределения и движения заключающихся в нём масс даётся основными уравнениями теории — уравнениями Эйнштейна.
Искривление пространства
(Псевдо)римановыми называются пространства, которые в малых масштабах ведут себя «почти» как обычные (псевдо)евклидовы. Так, на небольших участках сферы теорема Пифагора и другие факты евклидовой геометрии выполняются с очень большой точностью. В своё время это обстоятельство и позволило построить евклидову геометрию на основе наблюдений над поверхностью Земли (которая в действительности не является плоской, а близка к сферической). Это же обстоятельство обусловило и выбор именно псевдоримановых (а не каких-либо ещё) пространств в качестве основного объекта рассмотрения в ОТО: свойства небольших участков пространства-времени не должны сильно отличаться от известных из СТО.
Однако в больших масштабах римановы пространства могут сильно отличаться от евклидовых. Одной из основных характеристик такого отличия является понятие кривизны. Суть его состоит в следующем: евклидовы пространства обладают свойством абсолютного параллелизма: вектор X′,{\displaystyle X’,} получаемый в результате параллельного перенесения вектора X{\displaystyle X} вдоль любого замкнутого пути, совпадает с исходным вектором X.{\displaystyle X.} Для римановых пространств это уже не всегда так, что может быть легко показано на следующем примере. Предположим, что наблюдатель встал на пересечении экватора с нулевым меридианом лицом на восток и начал двигаться вдоль экватора. Дойдя до точки с долготой 180°, он изменил направление движения и начал двигаться по меридиану к северу, не меняя направления взгляда (то есть теперь он смотрит вправо по ходу). Когда он таким образом перейдёт через северный полюс и вернётся в исходную точку, то окажется, что он стоит лицом к западу (а не к востоку, как изначально). Иначе говоря, вектор, параллельно перенесённый вдоль маршрута следования наблюдателя, «прокрутился» относительно исходного вектора. Характеристикой величины такого «прокручивания» и является кривизна[11]
.
Решения уравнений Эйнштейна для чёрных дыр
Так как чёрные дыры являются локальными и относительно компактными образованиями, то при построении их теории обычно пренебрегают наличием космологической постоянной, так как её эффекты для таких характерных размеров задачи неизмеримо малы. Тогда стационарные решения для чёрных дыр в рамках ОТО, дополненной известными материальными полями, характеризуются только тремя параметрами: массой (M{\displaystyle M} ), моментом импульса (L{\displaystyle L} ) и электрическим зарядом (Q{\displaystyle Q} ), которые складываются из соответствующих характеристик вошедших в чёрную дыру при коллапсе и упавших в неё позднее тел и излучений (если в природе существуют магнитные монополи, то чёрные дыры могут иметь также магнитный заряд (G{\displaystyle G} )[12], но пока подобные частицы не обнаружены). Любая чёрная дыра стремится в отсутствие внешних воздействий стать стационарной, что было доказано усилиями многих физиков-теоретиков, из которых особо следует отметить вклад нобелевского лауреата Субраманьяна Чандрасекара, перу которого принадлежит фундаментальная для этого направления монография «Математическая теория чёрных дыр»[13]. Более того, представляется, что никаких других характеристик, кроме этих трёх, у не возмущаемой снаружи чёрной дыры быть не может, что формулируется в образной фразе Уилера: «Чёрные дыры не имеют волос»[12].
Решения уравнений Эйнштейна для чёрных дыр с соответствующими характеристиками:
- Решение Шварцшильда (1916 год, Карл Шварцшильд) — статичное решение для сферически-симметричной чёрной дыры без вращения и без электрического заряда.
- Решение Рейснера — Нордстрёма (1916 год, Ганс Рейснер и 1918 год, Гуннар Нордстрём) — статичное решение сферически-симметричной чёрной дыры с зарядом, но без вращения.
- Решение Керра (1963 год, Рой Керр) — стационарное, осесимметричное решение для вращающейся чёрной дыры, но без заряда.
- Решение Керра — Ньюмена (1965 год, Э. Т. Ньюмен (англ.), Э. Кауч, К. Чиннапаред, Э. Экстон, Э. Пракаш и Р. Торренс)[14] — наиболее полное на данный момент решение: стационарное и осесимметричное, зависит от всех трёх параметров.
Решение для вращающейся чёрной дыры чрезвычайно сложно. Его вывод был описан Керром в 1963 году очень кратко[15], и лишь спустя год детали были опубликованы Керром и Шильдом в малоизвестных трудах конференции. Подробное изложение вывода решений Керра и Керра — Ньюмена было опубликовано в 1969 году в известной работе Дебнея, Керра и Шильда[16]. Последовательный вывод решения Керра был также проделан Чандрасекаром более чем на пятнадцать лет позже[13].
Считается, что наибольшее значение для астрофизики имеет решение Керра, так как заряженные чёрные дыры должны быстро терять заряд, притягивая и поглощая противоположно заряженные ионы и пыль из космического пространства. Существует также гипотеза[17], связывающая гамма-всплески с процессом взрывной нейтрализации заряженных чёрных дыр путём рождения из вакуума электрон-позитронных пар (Р. Руффини с сотрудниками), но она оспаривается рядом учёных[18].
Теоремы об «отсутствии волос»
Теоремы об «отсутствии волос» у чёрной дыры (англ. No hair theorem) говорят о том, что у стационарной чёрной дыры внешних характеристик, помимо массы, момента импульса и определённых зарядов (специфических для различных материальных полей), быть не может (в том числе и радиуса), и детальная информация о материи будет потеряна (и частично излучена вовне) при коллапсе. Большой вклад в доказательство подобных теорем для различных систем физических полей внесли Брэндон Картер, Вернер Израэль, Роджер Пенроуз, Пётр Хрусьцель (Chruściel), Маркус Хойслер. Сейчас представляется, что данная теорема верна для известных в настоящее время полей, хотя в некоторых экзотических случаях, аналогов которых в природе не обнаружено, она нарушается[19].
Решение Шварцшильда
Основные свойства
Согласно теореме Биркгофа[en], гравитационное поле любого сферически симметричного распределения материи вне её даётся решением Шварцшильда. Поэтому слабо вращающиеся чёрные дыры, как и пространство-время вблизи Солнца и Земли, в первом приближении тоже описываются этим решением.
Две важнейшие черты, присущие чёрным дырам в модели Шварцшильда — это наличие горизонта событий (он по определению есть у любой чёрной дыры) и сингулярности, которая отделена этим горизонтом от остальной Вселенной[10].
Решением Шварцшильда точно описывается изолированная невращающаяся, незаряженная и не испаряющаяся чёрная дыра (это сферически симметричное решение уравнений гравитационного поля (уравнений Эйнштейна) в вакууме). Её горизонт событий — это сфера, радиус которой, определённый из её площади по формуле S=4πr2,{\displaystyle S=4\pi r^{2},} называется гравитационным радиусом или радиусом Шварцшильда.
Все характеристики решения Шварцшильда однозначно определяются одним параметром — массой. Так, гравитационный радиус чёрной дыры массы M{\displaystyle M}
ru-wiki.org
