сколько километров, среднее расстояние между центрами Земли и спутника, Википедия
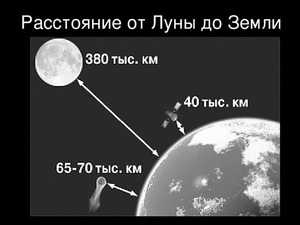 Луна представляет собой скалистое космическое тело сферической формы. На ней отсутствует атмосфера и любые признаки жизни. По сравнению с нашей планетой, единственным спутником которой она является. Диаметр спутника равен примерно четвёртой части диаметра Земли. Задолго до начала всевозможных исследований люди поняли, что Луна полна загадок и тайн.
Луна представляет собой скалистое космическое тело сферической формы. На ней отсутствует атмосфера и любые признаки жизни. По сравнению с нашей планетой, единственным спутником которой она является. Диаметр спутника равен примерно четвёртой части диаметра Земли. Задолго до начала всевозможных исследований люди поняли, что Луна полна загадок и тайн.
Она стоит в одном ряду с самыми крупными естественными спутниками планет солнечной системы. Плотность грунта относительно мала, а пробы, взятые с поверхности для детального анализа, приводят учёных в замешательство по сей день. По теории возникновения она «родилась» приблизительно 4,1 миллиарда лет назад.
Это интересно: Солнечная система, планеты по порядку и история названий.
Движение
Среднее расстояние от Луны до Земли составляет 384400 км, эта цифра приближенно включает в себя 60 радиусов нашей планеты. В зависимости от момента движения единственного спутника Земли по эллиптической орбите меняется степень её близости к планете и видимые наблюдателем размеры. При нахождении в перигее спутник от Земли отделяют 363104 километра. Когда небесное тело достигает апогея, кратчайшее
При наблюдении за движением этого небесного тела по небосводу можно попасть под влияние обмана зрения. Когда это оно находится высоко и окружено бесконечным пространством, его размеры воспринимаются значительно меньше, чем это есть в действительности. В непосредственной близости к горизонту Земли может показаться, что Луна обладает большим диаметром.
Ввиду того, что спутник то приближается к планете, то отдаляется от неё, варьируется и яркость поверхности Луны. Исследования доказывают, что спутник не создаёт свечения, а отражает порядка семи процентов рассеянного солнечного света. Эта особенность характеризуется реголитовым слоем, возникшим от столкновения с метеоритами. Частицы обломков имеют размеры от мельчайших до крупных и могут покрывать поверхность от нескольких микрон до десятков метров.
Это интересно: какая самая далекая от солнца планета?
От чего зависит движение
Движение Луны по орбите обусловлено влиянием на неё притяжением Земли и Солнца. Причём Солнце притягивает ее к себе в гораздо большей степени, чем наша планета. Помимо самой яркой звезды Солнечной системы, движение Луны есть совокупность многих параметров:
 Звёздный, или сидерический, месяц, который составляет 27 суток 7 часов 43 минуты и 11,51 секунды;
Звёздный, или сидерический, месяц, который составляет 27 суток 7 часов 43 минуты и 11,51 секунды;- По отношению к плоскости вращения Земли вокруг Солнца лунная орбита меняет угол наклона;
- Сама лунная орбита претерпевает изменения в точках перигея и апогея;
- Точки пересечения плоскостей орбит Луны и Солнца смещаются;
- Увеличение долготы перигея с периодом 8,8 лет;
- Орбита меняет свои габариты в апогее и перигее.
Перемещение Луны по орбите можно сравнить со спиралью, которая постепенно раскручивается.
Это интересно: красивые названия звёзд – история их появлений, названия звезд и созвездий.
Расстояние между Землёй и Луной
Расстояние между Землёй и Луной величина непостоянная. Древний учёный Гиппарх Никейский во втором веке до нашей эры сумел вычислить это расстояние. У него получилась цифра, равная тридцати земным диаметрам, то есть 384000 километров.
Величину диаметра смог измерить иной древнегреческий математик и астроном Эратосфен Киренский. Он установил шест в вертикальном положении около здания библиотеки и измерил длину отбрасываемой от него тени. Затем он определил наименьший угол, который образовывает солнечный луч, падая на шест. Получился градус, равный семи. Располагая знаниями о том, что в день летного солнцестояния в городе Сиене Солнце находится в зените, а расстояние от Сиены до Александрии составляет 5000 стадиев, Эратосфен сделал вывод: 5000 стадиев – это 7 градусов меридиана Земли. Полный меридиан равен 360 градусов, или примерно 250000 стадиев.
Это интересно: следствием осевого вращения Земли являются какие процессы?
Как узнать расстояние до спутника
Существует несколько методов измерения расстояния от Земли до Луны:
- Самый простой – на основании их угловых размеров.
Эти размеры одинаковы, так как во время полного солнечного затмения солнечный диск целиком заслоняется лунным. Для измерения подойдёт обычная лучинка. Если расположить лучинку в вытянутой руке, то отношение её ширины к длине до глаза есть угловой размер Луны в радианах. Данная величина равна 0,0087. При переведении радианов в градусы получится приблизительно 0,5. Зная радиус Земли и угловой размер нашего спутника, легко выяснить
- Методом лазерной локации.
 С поверхности Земли на рефлекторные отражатели, установленные на Луне астронавтами более сорока лет назад, направляется лазерный луч. Он движется с известной скоростью света и, достигнув рефлектора, возвращается назад. Путь луча составляет примерно одну секунду. Учёные фиксируют конкретное время и вычисляют точное расстояние до нашего спутника. Этот способ измерения помог установить, что ближайшее к Земле небесное тело меняет траекторию движения в сторону удаления от планеты на несколько сантиметров в год.
С поверхности Земли на рефлекторные отражатели, установленные на Луне астронавтами более сорока лет назад, направляется лазерный луч. Он движется с известной скоростью света и, достигнув рефлектора, возвращается назад. Путь луча составляет примерно одну секунду. Учёные фиксируют конкретное время и вычисляют точное расстояние до нашего спутника. Этот способ измерения помог установить, что ближайшее к Земле небесное тело меняет траекторию движения в сторону удаления от планеты на несколько сантиметров в год.
- Методом триангуляции (из двух равноудалённых на поверхности Земли точек).
Среднее расстояние до Луны: википедия
Ближайшая точка орбиты Луны расположена в среднем на расстоянии 362000 километров. Самая удалённая точка лунной орбиты находится на расстоянии 405000 километров.
Не менее двух раз в год в новолуние, когда спутник приближается максимально к узлу (точке пересечения с эклиптикой), имеет место солнечное затмение. В остальное время его движение осуществляется под Солнцем либо над ним. В полнолуния случаются лунные затмения, и естественный спутник Земли должен также быть рядом с узлом.
Прямая линия, соединяющая узлы, оборачивается вокруг нашей планеты каждые 18 лет и 224 дня. Направление вращения в данном случае противоположно ходу Луны.
Послесловие
 За столетие продолжительность земных суток увеличивается на одну тысячную долю секунды. Данное явление вызывает ближайшее к Земле небесное тело в результате действия сил гравитации. В мировом океане возникают отливы и приливы из-за гравитационного притяжения Луны, и эти процессы тормозят земное вращение.
За столетие продолжительность земных суток увеличивается на одну тысячную долю секунды. Данное явление вызывает ближайшее к Земле небесное тело в результате действия сил гравитации. В мировом океане возникают отливы и приливы из-за гравитационного притяжения Луны, и эти процессы тормозят земное вращение.
Гравитационное поле оказало влияние на форму небесного тела. На обращённой к Земле стороне присутствует деформация, хотя не исключается, что последняя возникла благодаря строению внутренних слоёв спутника.
Воздействие на Луну, производимое Землёй и Солнцем, модификации в траектории её движения по эллиптической орбите через миллионы лет отдалят таинственное небесное тело и оптически его уменьшат. Легендой станут и полные солнечные затмения.
obrazovanie.guru
Расстояние от Земли до Луны
 Луна с незапамятных времен была постоянным спутником нашей планеты и самым близким к ней небесным телом. Естественно, человеку всегда хотелось там побывать. Но далеко ли туда лететь и какое до нее расстояние?
Луна с незапамятных времен была постоянным спутником нашей планеты и самым близким к ней небесным телом. Естественно, человеку всегда хотелось там побывать. Но далеко ли туда лететь и какое до нее расстояние?
Что такое
Расстояние от Земли до Луны теоретически измеряется от центра Луны до центра Земли. Измерить это расстояние обычными методами, используемыми в обычной жизни, невозможно. Поэтому дистанция до земного спутника вычислялась по тригонометрическим формулам.
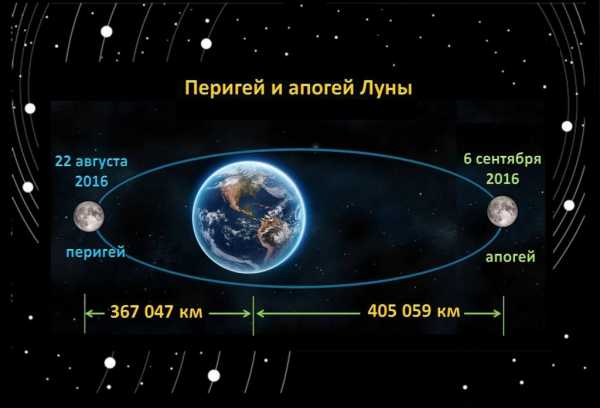
Перигей и апогей Луны
Аналогично Солнцу, Луна испытывает постоянное движение на земном небе вблизи эклиптики. Тем не менее, это движение значительно отличается от движения Солнца. Так плоскости орбит Солнца и Луны различаются на 5 градусов. Казалось бы, вследствие этого траектория Луны на земном небе должна быть похожа в общих чертах на эклиптику, отличаясь от нее только сдвигом на 5 градусов:
В этом движение Луна напоминает движение Солнца – с запада на восток, в противоположном направлении суточному вращению Земли. Но кроме того Луна движется по земному небу гораздо быстрее Солнца. Это связано с тем, что Земля совершает оборот вокруг Солнца примерно за 365 суток (земной год), а Луна вокруг Земли всего за 29 суток (лунный месяц). Это различие и стало стимулом к разбивке эклиптики на 12 зодиакальных созвездий (за один месяц Солнце смещается по эклиптике на 30 градусов). За время лунного месяца происходит полная смена фаз Луны:
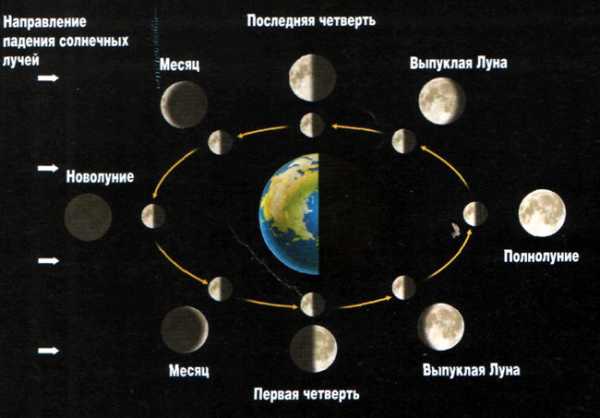
Лунные фазы
В дополнение к траектории движения Луны добавляется ещё и фактор сильной вытянутости орбиты. Эксцентриситет орбиты Луны составляет 0.05 (для сравнения у Земли этот параметр равен 0.017). Отличие от круговой орбиты Луны приводит к тому, что видимый диаметр Луны постоянно меняется от 29 до 32 угловых минут.
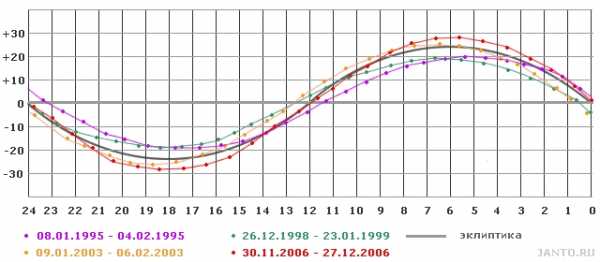
В конечном итоге траектория положения Луны на земном небе постоянно мигрирует относительно фоновых звезд и эклиптики
За сутки Луна смещается относительно звезд на 13 градусов, за час примерно на 0.5 градусов. Современные астрономы часто используют покрытия Луны для оценок угловых диаметров звезд вблизи эклиптики.
От чего зависит движение Луны
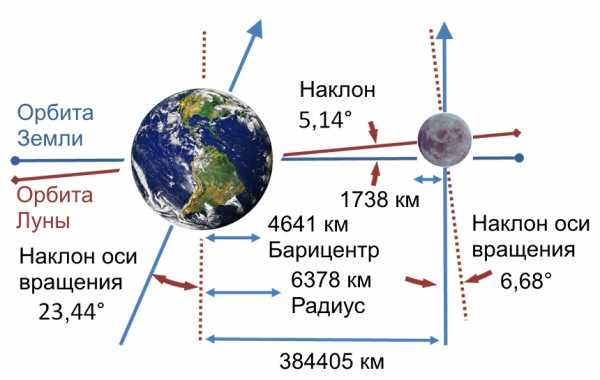 Важным моментом теории движения Луны является факт того, что орбита Луны в космическом пространстве не является неизменной и стабильной. По причине сравнительно небольшой массы Луны, она подвержена постоянным возмущениям от более массивных объектов Солнечной Системы (прежде всего Солнца и Луны). Кроме того, на орбиту Луны оказывают влияние сплюснутость Солнца и гравитационные поля других планет Солнечной Системы. В результате этого величина эксцентриситета орбиты Луны испытывает колебания между 0.04 и 0.07 с периодом в 9 лет. Следствием этих изменений стало такое явление, как суперлуние. Суперлунием называется астрономическое явление, в ходе которого полная луна в несколько раз больше по угловым размерам, чем обычно. Так во время полнолуния 14 ноября 2016 года Луна находилась на рекордно близком расстоянии с 1948 года. В 1948 году Луна была на 50 км ближе, чем в 2016 году.
Важным моментом теории движения Луны является факт того, что орбита Луны в космическом пространстве не является неизменной и стабильной. По причине сравнительно небольшой массы Луны, она подвержена постоянным возмущениям от более массивных объектов Солнечной Системы (прежде всего Солнца и Луны). Кроме того, на орбиту Луны оказывают влияние сплюснутость Солнца и гравитационные поля других планет Солнечной Системы. В результате этого величина эксцентриситета орбиты Луны испытывает колебания между 0.04 и 0.07 с периодом в 9 лет. Следствием этих изменений стало такое явление, как суперлуние. Суперлунием называется астрономическое явление, в ходе которого полная луна в несколько раз больше по угловым размерам, чем обычно. Так во время полнолуния 14 ноября 2016 года Луна находилась на рекордно близком расстоянии с 1948 года. В 1948 году Луна была на 50 км ближе, чем в 2016 году.

Сравнение видимого диаметра Луны на земном небе в перицентре и апоцентре лунной орбиты
Кроме того наблюдаются и колебания наклонения лунной орбиты к эклиптике: примерно на 18 угловых минут каждые 19 лет.
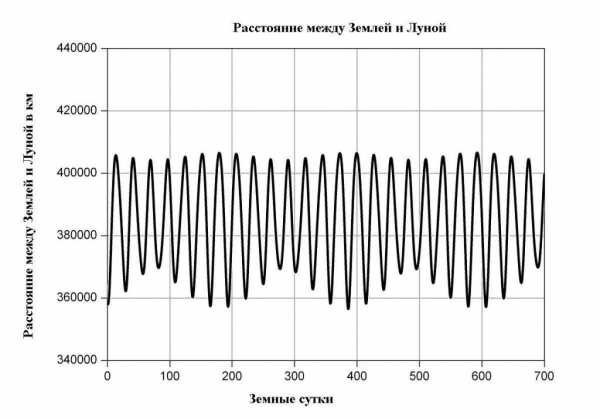
График изменения расстояния между Землей и Луной за 2 года
Чему равно

Свет от Земли до нашего спутника доберется очень быстро – за 1,255 секунд
Космическим кораблям придется потратить на полет к земному спутнику немало времени. До Луны нельзя лететь по прямой – планета будет уходить по орбите в сторону от точки назначения, и путь придется корректировать. При второй космической скорости в 11 км/с (40 000 км/ч) полет теоретически займет около 10 часов, но на деле это будет происходить дольше. Все потому, что корабль на старте постепенно наращивает скорость в атмосфере, доводя ее до значения в 11 км/с, чтобы вырваться из поля тяготения Земли. Затем кораблю придется тормозить при подлете к Луне. Кстати, эта скорость- максимум, чего удалось добиться современным космическим кораблям.
Пресловутый полет американцев на Луну в 1969 году, согласно официальным данным, занял 76 часов. Быстрее всех до Луны удалось долететь аппарату НАСА «Новые горизонты» — за 8 часов 35 минут. Правда, он не приземлился на планетоид, а пролетел мимо – у него была другая миссия.
Свет от Земли до нашего спутника доберется очень быстро – за 1,255 секунд. Но полеты на световых скоростях – пока что из области фантастики.
Можно попытаться представить путь до Луны в привычных величинах. Пешком при скорости 5 км/ч дорога до Луны займет порядка девяти лет. Если поехать на машине на скорость в 100 км/ч, то добираться до земного спутника придется 160 дней. Если бы на Луну летали самолеты, то рейс до нее продлился бы где-то 20 дней.
Как в древней Греции астрономы рассчитывали расстояние до Луны
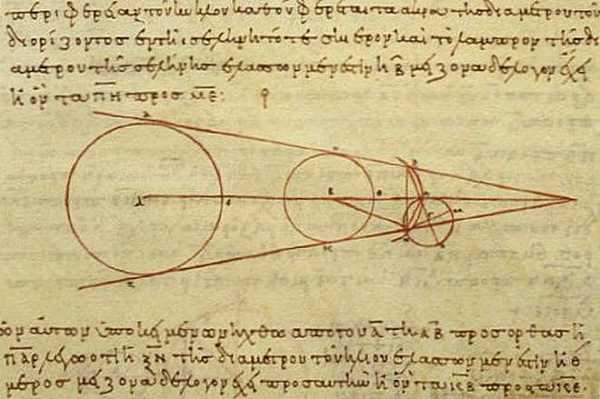
Расстояние от Земли до Луны
Луна стала первым небесным телом, до которого удалось рассчитать расстояние от Земли. Считается, что первыми это сделали астрономы в Древней Греции.
Измерить расстояние до Луны пытались с незапамятных времен – первым это попытался сделать Аристарх Самосский. Он оценил угол между Луной и Солнцем в 87 градусов, поэтому вышло, что Луна ближе Солнца в 20 раз (косинус угла равного 87 градуса равен 1/20). Ошибка измерений угла привела к 20-кратной ошибке, сегодня известно, что это отношение на самом деле равно 1 к 400 (угол равен примерно 89.8 градусов). Большая ошибка была вызвана трудностью оценок точного углового расстояния между Солнцем и Луной с помощью примитивных астрономических инструментов Древнего мира. Регулярные солнечные затмения к этому времени уже позволили древнегреческим астрономам сделать вывод о том, что угловые диаметры Луны и Солнца примерно одинаковы. В связи с этим Аристарх сделал вывод, что Луна меньше Солнца в 20 раз (на самом деле примерно в 400 раз).
Для вычисления размеров Солнца и Луны относительно Земли Аристарх использовал другой метод. Речь идет о наблюдениях лунных затмений. К этому времени древние астрономы уже догадались о причинах этих явлений: Луна затмевается тенью Земли.
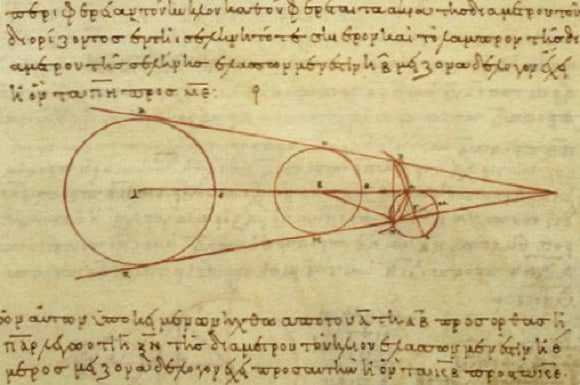
На схеме выше хорошо видно, что разность расстояний с Земли до Солнца и до Луны пропорциональна разнице между радиусами Земли и Солнца и радиусами Земли и её тени на расстояние Луны. Во времена Аристарха уже удалось оценить, что радиус Луны равен примерно 15 угловым минутам, а радиус земной тени составляет 40 угловых минут. То есть размер Луны получался примерно в 3 раза меньше размера Земли. Отсюда зная угловой радиус Луны можно было легко оценить, что Луна находится от Земли примерно в 40 диаметрах Земли. Древние греки могли лишь приблизительно оценить размеры Земли. Так Эратосфен Киренский (276 – 195 годы до нашей эры) на основе различий в максимальной высоте Солнца над горизонтом в Асуане и Александрии во время летнего солнцестояния определил, что радиус Земли близок к 6287 км (современное значение 6371 км). Если подставить это значение в оценку Аристарха насчет расстояния до Луны, то оно будет соответствовать примерно 502 тысяч км (современное значение среднего расстояния от Земли до Луны составляет 384 тысяч км).
Чуть позже математик и астроном II века до н. э. Гиппарх Никейский подсчитал, что расстояние до земного спутника в 60 раз больше, чем радиус нашей планеты. Его расчеты основывались на наблюдениях за движением Луны и его периодических затмениях.
Материалы по теме

Так как в момент затмения Солнце и Луна будут иметь одинаковые угловые размеры, то по правилам подобия треугольников можно найти отношение расстояний до Солнца и до Луны. Эта разница составляет 400 раз. Применяя еще раз эти правила, только уже по отношению к диаметрам Луны и Земли, Гиппарх вычислил, что диаметр Земли больше диаметра Луны в 2,5 раза. Т.е Rл = Rз/2,5.
Под углом в 1′ можно наблюдать предмет, размеры которого в 3 483 раза меньше, чем расстояние до него – эта информация во времена Гиппарха была всем известна. То есть, при наблюдаемом радиусе Луны в 15′ она будет ближе к наблюдателю в 15 раз. Т.е. отношение расстояния до Луны к ее радиусу будет равно 3483/15= 232 или Sл= 232Rл.
Соответственно, дистанция до Луны – это 232* Rз /2,5= 60 радиусов Земли. Это получается 6 371*60=382 260 км. Самое интересное, что измерения, выполненные при помощи современных инструментов, подтвердили правоту античного ученого.
Сейчас измерение дистанции до Луны проводится при помощи лазерных приборов, позволяющих измерить его с точностью до нескольких сантиметров. При этом измерения происходят за очень короткое время – не более 2 секунд, за которое Луна удаляется по орбите примерно на 50 метров от точки отправки лазерного импульса.
Эволюция методик измерения расстояния до Луны
Только с изобретением телескопа астрономы смогли получить более-менее точные значения параметров орбиты Луны и соответствия её размеров с размером Земли.
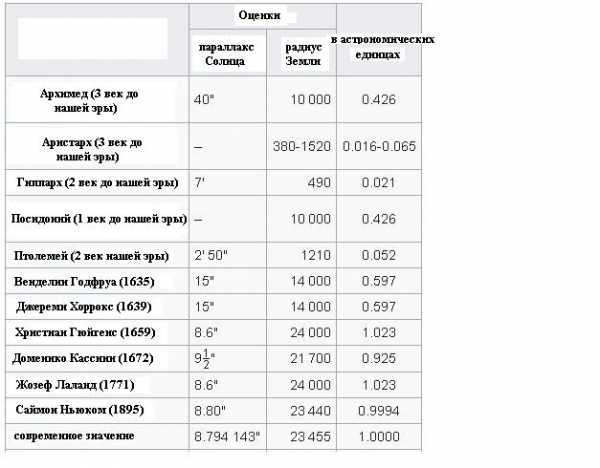
Пример эволюции астрономической единицы со временем
Более точный метод измерения расстояния до Луны появился в связи с развитием радиолокации. Первая радиолокация Луны была проведены в 1946 году в США и Великобритании. Радиолокация позволяла измерить расстояние до Луны с точностью в несколько километров.
Ещё более точным методом измерения расстояния до Луны стала лазерная локация. Для его реализации в 1960х годах на Луне было установлено несколько уголковых отражателей. Интересно отметить, что первые эксперименты по лазерной локации были проведены ещё до установки уголковых отражателей на поверхности Луны. В 1962-1963 годах в Крымской обсерватории СССР были проведены несколько экспериментов по лазерной локации отдельных лунных кратеров с использованием телескопов диаметром от 0.3 до 2.6 метров. Эти эксперименты смогли определять расстояние до поверхности Луны с точностью в несколько сотен метров. В 1969-1972 годы астронавты программы “Аполлон” доставили на поверхность нашего спутника три уголковых отражателя. Среди них наиболее совершенным был отражатель миссии “Апполон-15”, так как он состоял 300 призм, тогда как два других (миссии “Апполон-11” и “Апполон-14”) только из ста призм каждый.

Карта положения уголковых отражателей
Кроме того в 1970 и 1973 годах СССР доставил на поверхность Луны ещё два французских уголковых отражателя на борту самоходных аппаратов “Луноход-1” и “Луноход-2”, каждый из которых состоял из 14 призм. Использование первого из этих отражателей обладает незаурядной историей. За первые 6 месяцев работы лунохода с отражателем удалось провести около 20 сеансов лазерной локации. Однако затем из-за неудачного положения лунохода вплоть до 2010 года не удавалось использовать отражатель. Лишь снимки нового аппарата LRO помогли уточнить положение лунохода с отражателем, и тем самым возобновить сеансы работы с ним.
В СССР наибольшее количество сеансов лазерной локации было проведено на 2.6-метровом телескопе Крымской обсерватории. Между 1976 и 1983 годами на этом телескопе было проведено 1400 измерений с погрешностью в 25 сантиметров, затем наблюдения были прекращены в связи со свертыванием советской лунной программы.
Всего же с 1970 по 2010 годы в мире было проведено примерно 17 тысяч высокоточных сеансов лазерной локации. Большинство из них было связано с уголковым отражателем “Аполонна-15” (как говорилось выше, он является наиболее совершенным – с рекордным количеством призм):
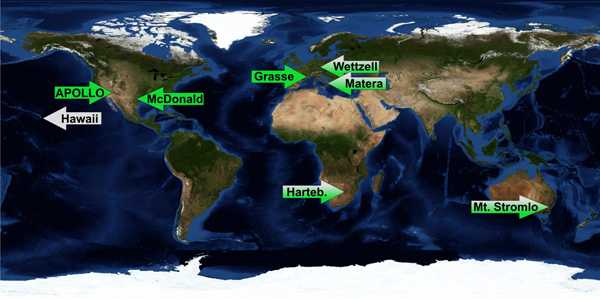
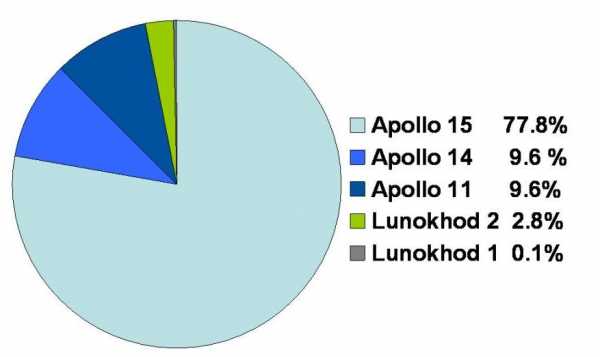 Из 40 обсерваторий, способных выполнять лазерную локацию Луны лишь несколько могут выполнять высокоточные измерения:
Из 40 обсерваторий, способных выполнять лазерную локацию Луны лишь несколько могут выполнять высокоточные измерения:
 Большинство сверхточных измерений выполнено на 2-метровом телескопе в техасской обсерватории имени Мак Дональда:
Большинство сверхточных измерений выполнено на 2-метровом телескопе в техасской обсерватории имени Мак Дональда:
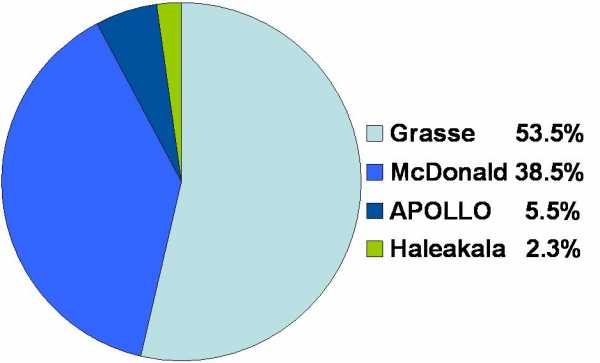
В то же время наиболее точные измерения выполняет инструмент APOLLO, который был установлен на 3.5-метровом телескопе обсерватории Апач Пойнт в 2006 году. Точность его измерений достигает одного миллиметра:
 Эволюция системы Луна и Земля
Эволюция системы Луна и Земля
Главной целью всё более точных измерений расстояния до Луны являются попытки более глубокого понимания эволюции орбиты Луны в далеком прошлом и в отдаленном будущем. К настоящему времени астрономы пришли к выводу, что в прошлом Луна находилась в несколько раз ближе к Земле, а так же обладала значительно более коротким периодом вращения (то есть не была приливно захваченной). Этот факт подтверждает импактную версию образования Луны из выброшенного вещества Земли, которая преобладает в наше время. Кроме того, приливное воздействие Луны приводит к тому, что скорость вращения Земли вокруг своей оси постепенно замедляется. Скорость этого процесса составляет увеличение земных суток каждый год на 23 микросекунды. За один год Луна отдаляется от Земли в среднем на 38 миллиметров. Оценивается, что в случае если система Земля-Луна переживет превращение Солнца в красный гигант, то через 50 миллиардов лет земные сутки сравняются с лунным месяцем. В результате Луна и Земля будут всегда повернуты к друг другу только одной стороной, как сейчас наблюдается в системе Плутон-Харон. К этому времени Луна отдалится до, примерно, 600 тысяч километров, а лунный месяц увеличится до 47 суток. Кроме того, предполагается, что испарение земных океанов через 2.3 миллиардов лет приведет к ускорению процесса удаления Луны (земные приливы значительно тормозят процесс).
Кроме того, расчеты показывают, что в дальнейшем Луна снова начнет сближаться с Землей по причине приливного взаимодействия с друг другом. При приближении к Земле на 12 тысяч км Луна будет разорвана приливными силами, обломки Луны образуют кольцо наподобие известных колец вокруг планет-гигантов Солнечной Системы. Другие известные спутники Солнечной Системы повторят эту судьбу гораздо раньше. Так Фобосу отводят 20-40 миллионов лет, а Тритону около 2 миллиардов лет.
Интересные факты

Между Землей и Луной можно поместить все остальные планеты Солнечной системы
Каждый год расстояние до земного спутника возрастает в среднем на 4 см. Причины – движение планетоида по спиральной орбите и постепенно падающая мощность гравитационного взаимодействия Земли и Луны.
Между Землей и Луной теоретически можно разместить все планеты Солнечной системы. Если сложить диаметры всех планет, включая Плутон, то получится величина в 382 100 км.
comments powered by HyperComments
Понравилась запись? Расскажи о ней друзьям!
Просмотров записи: 4106
spacegid.com
Расстояние от Земли до Луны
Солнечная система > Система Земля-Луна > Спутник Луна > Расстояние от Земли до Луны
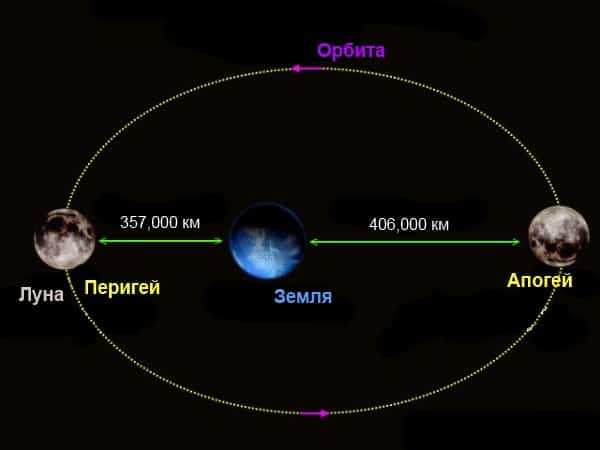
Расстояние от Земли до Луны
Какая дистанция от Земли до Луны: самое близкое и дальнее расстояния между космическими телами. Узнайте, сколько планет поместятся между Землей и Луной на фото.
Если коротко, то расстояние от Земли до Луны в среднем составляет 384403 км. Но важно знать несколько нюансов. Мы не зря употребили слово «средний», потому что Луна проходит по эллиптическому пути и меняет удаленность.
Самое близкое и далекое расстояние от Земли до Луны
В ближайшей точке показатель составляет 363104 км, а при максимальной отдаленности – 406696 км. Вы видите разницу в 43592 км, что довольно много. От этого меняется и ее кажущийся размер на 15%. Также сказывается на светимости, ведь она будет казаться на 30% ярче в полной фазе и при максимальном сближении. Этот момент именуют суперлуной.
Записи древних греков о размере Луны
Это видео выпустили в 2011 году, чтобы отобразить геоцентрическую фазу, угол осевой позиции, либрацию и кажущийся лунный диаметр за год.
Но как нам вообще удалось определить дистанцию? Ну, все зависит от времени вычисления. Древние греки полагались на простые геометрические формулы. Они долгое время отслеживали изменение теней и догадались, что она должна быть в 108 раз больше диаметра тела. Отсюда возникли идеи о затмениях.

Сравнение видимых размеров Луны в Апогей и Перигей
Ученые выяснили, что тень примерно в 2.5 раз больше лунной ширины. Сам объект обладает достаточными параметрами, чтобы периодически закрывать от нас Солнце. Зная земной диаметр и формулу треугольника, они вывели дистанцию в 397500 км. Не совсем точно, но это удивительные показатели для того времени.
Сейчас мы используем миллиметровое измерение – вычисление времени, за которое сигнал движется от Земли к объекту. Благодаря миссии Аполлон нам удалось провернуть это со спутником. Более 40 лет назад астронавты установили на его поверхности специальные отражающие зеркала, в которые с нашей планеты посылают лазерные лучи. Мы получаем слабую отдачу, но этого хватает, чтобы вывести максимально точное число.
Световая скорость составляет 300000 км/с, поэтому для преодоления пути нужно чуть больше секунды. Далее уходит еще столько же на возврат. Также эта техника помогла понять, что каждый год спутник отдаляется на 3.8 см, и через миллиарды лет он будет визуально казаться меньше звезды. Да, придется попрощаться с любимыми затмениями.
Между Землей и Луной можно разместить все планеты

Если вспомнить о масштабах наших планет (особенно газовых гигантов), то удивляешься, что это может быть реальным. Чтобы понять, давайте взглянем на планетарные диаметры:
- Меркурий – 4879 км
- Венера – 12104 км
- Марс – 6771 км
- Сатурн – 116464 км
- Уран – 50724 км
- Нептун – 49244 км
- Всего: 380008 км
Дистанция между нами и спутником составляет 384400 км. Получается, что мы еще и экономим 4392 км. Что же сделать с остатком? Ну, можно добавить Плутон, простирающийся на 2092 км, а также еще какую-нибудь карликовую планету. Конечно, физически они бы не смогли вращаться рядом, но сама возможность удивляет.
Читайте также:
Положение и движение Луны
Строение Луны
Поверхность Луны
v-kosmose.com
Эволюция расстояния между Луной и Землёй / О. Г. Сорохтин: «Развитие Земли» / Земля
Существенное влияние на приливное взаимодействие планет оказывает эффективная механическая добротность Q центральной планеты. Напомним, что под фактором добротности понимается степень приближения реологических свойств реальных тел к идеальной упругости: чем выше механическая добротность тела, тем его свойства ближе к идеально упругим материалам и, наоборот, чем ниже фактор добротности, тем это тело больше проявляет свои вязкие свойства. Ярким примером тела с высокой добротностью может служить долго звучащий бронзовый колокол, если же такой колокол сделать из пластилина, то вообще никакого звучания не будет, так как в этом случае вся энергия удара полностью переходит в пластические деформации. Численно безразмерный фактор добротности равен отношению общей энергии, затрачиваемой на деформацию тела (например, за счёт приливных взаимодействий планет), к той её части, которая благодаря процессам внутреннего трения в материале этого тела, превращается в тепло.Теория приливных взаимодействий планет показывает, что если угловая скорость осевого вращения центральной планеты превышает угловую скорость орбитального обращения спутника (как это и наблюдается в системе Земля-Луна), то благодаря таким взаимодействиям осевое вращение центральной планеты будет тормозиться, а спутник будет от неё отодвигаться. При этом скорость удаления спутника от центральной планеты оказывается пропорциональной его массе, обратно пропорциональной фактору добротности центральной планеты и расстоянию между ними в степени 5,5. Таким образом, для расчёта эволюции системы Земля-Луна и определения зависимости расстояния между планетами от времени предварительно необходимо выяснить, как менялась эффективная механическая добротность Земли Q, определяемая выражением (6), за всю историю её развития. Задача эта непростая, однако, в первом приближении, на уровне оценок вполне решаемая.
Молодая Земля сразу же после своего образования была холодным космическим телом, и в ее недрах температура ещё нигде не превышала температуру плавления вещества. Об этом, в частности, свидетельствует полное отсутствие на Земле изверженных (да и любых других) пород старше 4 млрд лет. Об этом же говорят изотопно-свинцовые отношения, показывающие, что процессы дифференциации земного вещества начались значительно позже образования самой Земли и (в противоположность Луне) протекали без существенного плавления. Кроме того, на земной поверхности тогда не было ни океанов, ни атмосферы. Поэтому эффективная механическая добротность Земли в тот ранний период её развития, который в дальнейшем будем называть катархейским, была сравнительно высокой. По сейсмическим данным, в развитой океанической литосфере, т. е. в холодном земном веществе мантийного состава, фактор добротности находится в пределах от 1 000 до 2 000, тогда как в частично расплавленной астеносфере под океанами его значение снижается до 100. В холодной верхней мантии Луны этот фактор приблизительно равен 5 000, а в более прогретой средней мантии снижается до 1 500 (Жарков, 1983).
В отличие от современных условий молодая Земля, как уже отмечалось, была существенно холоднее, лишена астеносферы и ядра, и даже могла характеризоваться отрицательным градиентом температуры в нижней мантии (рис. 29). Поэтому в те далёкие времена механическая добротность Земли в её глубинных недрах скорее всего существенно превышала фактор добротности современной литосферы. Однако следует учитывать, что на приливное взаимодействие планет в основном влияют слои с наименьшими значениями фактора добротности. Учитывая сказанное и для определённости расчётов, примем, что в течение всего катархея, т.е. от момента образования Земли, приблизительно 4,6 млрд лет назад, и вплоть до начала развития в ней геологических процессов в самом начале архея, около 4 млрд. лет назад, значение приливного фактора добротности Земли равнялся 1 500.
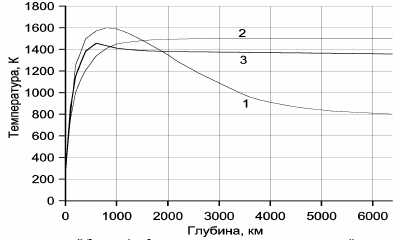
Рисунок 29. Температура молодой Земли: 1 и 2 предельные распределения начальной температуры Земли:
1 — по В. С. Сафронову (1969) с учётом ударов тел разных размеров, но вначале мелких, а затем и более крупных; 2 — по А. В. Витязеву и др. (1990) с учётом ударов крупных тел в начале процесса аккреции Земли; 3 — принятое распределение начальной температуры Земли, учитывающее как ударное нагревание планеты, так и её приливное разогревание при захвате и разрушении Протолуны.
Приведённая оценка фактора добротности Земли в катархее позволяет определить, что за этот период Луна благодаря приливным взаимодействиям с Землёй оказалась отброшенной от предела Роша (около 17 тыс. км) на расстояние до 160 тыс. км (рис. 26). При этом отодвигание Луны от Земли было неравномерным: вначале очень быстрым, а затем более спокойным.
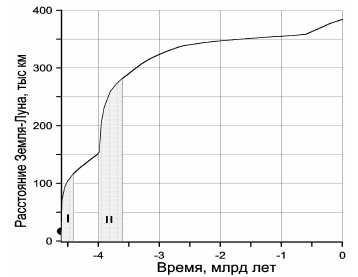
Рисунок 26. Эволюция расстояния между Луной и Землёй.
Интервал I — время развития на Луне анортозитового магматизма; интервал II — время развития базальтового магматизма на Луне (пояснения в тексте).
Количественная модель изменения фактора добротности Земли в остальные периоды геологического времени может быть рассчитана с привлечением эмпирических данных. В частности, средние значения фактора добротности в фанерозое и протерозое могут быть определены по палеонтологическим данным, позволяющим найти для некоторых моментов времени этих эпох число дней в году или, что то же, угловую скорость собственного вращения Земли. Так, по суточной микрослоистости девонских кораллов Дж. Уэллс (1963) показал, что в среднем девоне год состоял приблизительно из 400 сут., а продолжительность суток не превышала 22 ч. В дальнейшем аналогичные определения были выполнены и для других периодов фанерозоя, а также для строматолитов — отложений бактериальных и микроводорослевых плёнок раннего протерозоя (рис. 28).
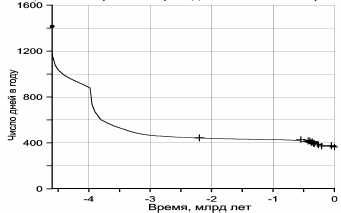
Рисунок 28. Изменение числа дней в году в связи с эволюцией расстояния между Землёй и Луной.
Крестиками показаны эмпирические определения числа дней в году по микрослоистости коралловых построек в фанерозое и строматолитов формации Ганфлинт (2,2 млрд. лет назад) в протерозое (Panella, 1972).
Зная современное расстояние Луны от Земли (384,4 тыс. км), далее удаётся уже рассчитать среднее значение фактора добротности в фанерозое, т.е. за последние 600 млн лет. Оно оказалось приблизительно равным 12. Полученная оценка неплохо совпала с независимым определением приливного фактора добротности Земли около 13, выполненным Г. Макдональдом (1964) на основании обработки данных по современным приливам в океанах и морях. Низкие значения приливного фактора добротности в фанерозое объясняются широким развитием в эту геологическую эпоху мелководных эпиконтинентальных морей, покрывающих сейчас на шельфах около 30% континентальной коры. Но именно в мелководных морях и происходит основное рассеивание энергии приливов за счёт трения приливных течений о дно мелководных бассейнов.
Аналогичным путём по суточной микрослоистости строматолитов в раннем протерозое возрастом около 2,2 млрд лет Г. Паннелла (1972) определил, что тогда в году было 445 сут., а продолжительность самих суток была менее 20 ч (рис. 28). Откуда удаётся определить, что в протерозое фактор приливной добротности Земли равнялся приблизительно 75. Повышенное значение фактора добротности в протерозое вполне понятно, поскольку в ту далёкую эпоху уже образовался глубокий океан, а мелководных эпиконтинентальных морей тогда ещё почти не существовало. Но диссипация приливной энергии в глубоком океане мала, поскольку в этом случае не возникают сильные придонные течения — основная причина приливного торможения Земли.
В архее приливная добротность Земли, как и в фанерозое, должна была быть достаточно низкой по двум причинам. Во-первых, тогда сами океаны ещё были мелкими и в них рассеивалась значительная часть приливной энергии и, во-вторых, в архее уже происходило расплавление верхней мантии (во всяком случае на низких широтах) с существенным её перегревом. Учитывая теперь неразрывность процесса отодвигания Луны от Земли и связывая его воедино в катархее, архее, протерозое и фанерозое, можно определить, что в архее фактор приливной добротности Земли в среднем равнялся 26.
Итак, полученная упрощённая модель изменения фактора добротности Земли Q, основанная на комбинации теоретических соображений с расчётами по эмпирическим данным, выглядит следующим образом: в катархее (от 4,6 до 4,0 млрд лет назад) Q = 1 500; в архее (от 4,0 до 2,6 млрд лет назад) Q = 26; в протерозое (от 2,6 до 0,6 млрд лет назад) Q = 75: в фанерозое (приблизительно от 600 млн лет назад до настоящего времени) Q = 12. Реальное распределение фактора добротности по времени, безусловно, могло меняться по более сложному закону, но основные его черты в приведённом распределении, по-видимому, определены все-таки правильно.
Уточнить приведённую модель возможно, если учесть, что результирующая приливная добротность Земли определяется суммой диссипативных функций мантии и гидросферы, а сами эти функции обратно пропорциональны факторам добротности рассматриваемых геосфер. Кроме того, следует отдельно учитывать приливные диссипативные функции для мантии под океанами (Q ~ 150) и континентами (Q ~ 500), а также для глубоких океанов и мелководных эпиконтинентальных морей, при этом факторы добротности для них можно считать пропорциональными содержащимся в них массам воды. В предыдущих работах (Сорохтин, Ушаков, 1991, 1993) были рассчитаны массы континентальной коры, воды в океанах и средние глубины океанов для всех прошлых геологических эпох. Это позволило нам рассчитать количественную модель зависимости фактора добротности Земли от времени, причём отдельно для гидросферы, мантии и всей Земли в целом. При этом принималось, что в архее и протерозое ещё не существовало мелководных эпиконтинентальных морей, происхождение же архейских мелководных морских бассейнов на океанической коре просто объясняется малыми количествами воды в океанах того времени. Объёмы эпиконтинентальных морей фанерозоя были оценены по палеореконструкциям континентов и площадям распространения морских осадков на континентах.
Построенная по этим условиям уточнённая кривая распределения фактора добротности во времени приведена на рис. 25. Рассчитанная по этой модели зависимость расстояния между центрами тяжести Земли и Луны от времени приведена на рис. 26.
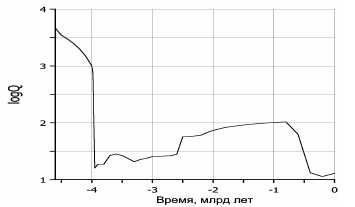
Рисунок 25. Зависимость фактора приливной добротности Земли от времени,
построенная с учётом данных по накоплению воды в океанах и по распространению эпиконтинентальных морей в фанерозое
Первое, на что следует обратить внимание в рассматриваемой модели, это совпадение времени эволюции лунной орбиты с возрастом самих планет. Такой вывод сегодня представляется естественным, но не следует забывать, что классические модели приливного взаимодействия Луны с Землёй обычно приводили к слишком короткой продолжительности их нормальной эволюции (около 1,8 млрд лет). Связано это было с тем, что в таких моделях современное низкое значение фактора добротности распространялось на всю историю развития Земли. В результате для выхода из явного противоречия с возрастом образования нашей планетной системы авторам таких гипотез приходилось прибегать к весьма экзотическим представлениям. Так, немецкий учёный Г. Герстенкорн (1955, 1967) считал, что Луна первоначально вращалась в обратном направлении и около 1,8 млрд лет назад подходила к Земле почти на расстояние предела Роша, но затем, после перехода через полярную орбиту, когда её вращение стало прямым, вновь начала удаляться от Земли.
Известный американский геофизик В. Манк (1968) образно описал развитие гипотетического «события Герстенкорна». По его оценкам, в короткий период наибольшего сближения Луны с Землёй океанские приливы должны были достигать высоты 1 км, и каждые 3 ч они обрушивались бы на континенты, приводя к их выравниванию. В это время диссипация (рассеивание) энергии лунных приливов была бы столь высокой, что все земные океаны вскипели бы и испарились, образовав вокруг Земли мощную атмосферу из водяного пара. При этом с учётом парникового эффекта температура у поверхности Земли поднялась бы до 1 000 °С, погубив тем самым любые проявления жизни. К этой страшной картине добавим ещё, что при столь высоких температурах произошла бы почти полная диссоциация (распад) карбонатов — известняков и доломитов с выделением в атмосферу огромных количеств углекислого газа. В результате в земной атмосфере, подобно Венере, возник бы необратимый парниковый эффект с подъёмом приземной температуры до 500-600 °С со всеми вытекающими последствиями.
Безусловно, описываемая катастрофическая ситуация оставила бы свой неизгладимый след в летописи геологической истории Земли, однако таких следов нигде не обнаружено, да и мы живём в комфортабельных климатических условиях, а не в «паровом котле». Это убедительно говорит о том, что «событие Герстенкорна» вовсе не существовало, а начало нормальной эволюции системы Земля-Луна совпадает по времени с моментом их образования как системы двойной планеты около 4,6 млрд лет назад, когда океанов на Земле ещё не существовало.
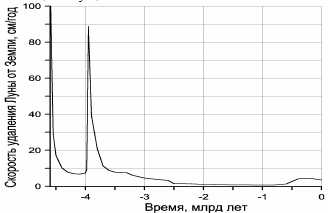
Рисунок 27. Скорость удаления Луны от Земли, см/год.
Масштаб рисунка не позволил привести максимальные значения этой скорости: около 4,6 млрд лет назад она достигала 12×106 см/год, или около 12 км/год, однако уже через 1 млн лет она снизилась до 9,64 м/год, а через 10 млн лет — до 1,37 м/год; в настоящее время Луна отодвигается от Земли со средней скоростью около 3,4 см/год.
Второе обстоятельство, на которое следует обратить внимание, — это неравномерность отодвигания Луны от Земли (рис. 27). С наибольшими скоростями (около 12-10 км/год) Луна отодвигалась от Земли в самом начале своего эволюционного пути (сразу же после разрушения её материнской планеты — Протолуны), около 4,6 млрд лет назад. Однако скорость отодвигания Луны от Земли тогда быстро уменьшалась и уже через 1 млн лет она снизилась до 9,64 м/год, а ещё через 10 млн лет она упала до 1,37 м/год. К концу катархея, около 4 млрд лет назад, скорость удаления Луны от Земли уже не превышала 4,3 см/год. Второй значительный импульс резкого увеличения скорости отодвигания Луны (до 90 см/год) возник на рубеже катархея и архея около 3,9 млрд лет тому назад. Наконец, третий период относительного ускорения отодвигания Луны от Земли, правда, с существенно меньшими скоростями (около 3,4 см/год), приходится на фанерозой. При этом только первый импульс стремительного удаления спутника от планеты был связан с малым исходным расстоянием их образования (напомним, что скорость отодвигания Луны от Земли обратно пропорциональна расстоянию в степени 5,5). Природа же второго и третьего импульсов ускорения была вызвана чисто земными событиями. Архейский пик был связан с началом формирования тогда астеносферы и океанов на Земле, а фанерозойское увеличение скорости отодвигания Луны от Земли — с подъёмом поверхности растущего океана до среднего уровня континентальных шельфов, после чего на континентальной коре возникли многочисленные мелководные эпиконтинентальные моря, в которых и рассеивается основная часть приливной энергии.
Интересно теперь сопоставить полученные результаты с имеющимися эмпирическими данными. Такие данные предоставляет нам палеонтология (о чем уже было сказано выше). Результаты теоретического расчёта эволюции числа дней в году, проведённого по несколько сглаженной модели фактора добротности Q, показаны на рис. 28. На этот же график нанесены все эмпирические данные по определению числа дней в году, полученные на основании изучения микрослоистости кораллов и строматолитов (Шопф, 1982). Как видно из сопоставления теоретической кривой с такими определениями, получено неплохое совпадение теории с экспериментом. Это придаёт уверенность в том, что наши расчёты приводят в основном к верным результатам.
www.gemp.ru
Расстояние от Земли до Луны
Солнечная система > Система Земля-Луна > Спутник Луна > Расстояние от Земли до Луны
Если говорить кратко, среднее расстояние от Земли до Луны составляет 384 403 км (238857 миль). Но прежде чем продолжить вам нужно понять еще несколько моментов. Для начала, обратите внимание на использование слова «среднее». Оно связано с тем, что орбита Луны, по которой она движется вокруг Земли, имеет эллиптическую форму. Это означает, что в определенное время она будет отдаляться от нашей планеты, а потом наоборот приближаться.
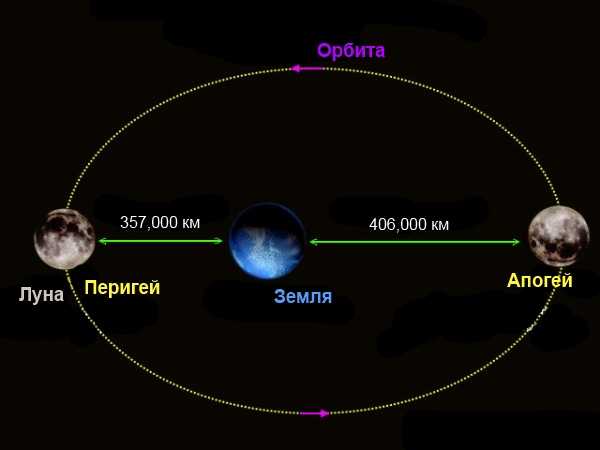
Расстояние от Земли до Луны
Следовательно, число 384403 км, это расстояние, которое астрономы называют большой полуосью. В ближайшей точке (известной как перигея) Луна находится всего в 357 104 км (225622 миль) от Земли. А в самой отдаленной (так называемой апогее) Луна находится от нас на расстоянии 406696 км (252088 миль).
Это означает, что расстояние от Земли до Луны может варьироваться в пределах 43592 км. Разница довольно большая, и это может объяснить тот факт, что в разное время наш спутник сильно отличается по своим размерам, которые зависят от того, на каком участке орбиты он находится. Например, ее размер в самой дальней и ближней точке может изменяться на 15%. Расстояние также может иметь огромное влияние на яркость Луны в полной фазе. Как и следовало ожидать, самые яркие полные Луны происходят, когда спутник находится в ближайшей к нам точке. В таком случае ее свет будет на 30% мощнее, чем в апогее. Подобное полнолуние известно, как суперлуние (техническое название – перигей-Сигизий).

Сравнение видимых размеров Луны в Апогей и Перигей
Для того чтобы получить представление о том, как все это выглядит, в 2011 году научной студией визуализации цента космических полетов имени Годдарда была выпущена специальная анимация. Она показывает геоцентрическую фазу, либрацию, угол положения оси, и видимый диаметр Луны в течение года, с разными часовыми интервалами.
Сейчас можно задать очень хороший вопрос: откуда мы знаем, как далеко находится Луна? Ответ зависит от времени, когда его произносят. В дни Древней Греции астрономы полагались на простую геометрию: с помощью радиуса Земли, размер которого они уже рассчитали (12875 км или 8000 миль) и измерений теней, они смогли достичь первых относительно точных результатов.
Наблюдая и записывая, как тени меняются в течение длительного периода истории, древние греки определили, что когда объект находится в передней части Солнца, длина его тени всегда будет в 108 раз больше диаметра самого объекта. Так мяч диаметром 2,5 см (1 дюйм), размещенный на палочке между Солнцем и Землей будет создавать треугольную тень, которая проходит на 270 см (108 дюймов).
Это рассуждение также применялось к лунным и солнечным затмениям.
В первом случае они обнаружили, что Луна не полностью блокировалась тенью Земли, и ее ширина была 2,5 раза больше ширины спутника. В последнем, они отметили, что Луна имела достаточный размер и находилась на нужном расстоянии для того, чтобы полностью закрыть собой Солнце. Более того, тень, которую она отбрасывает на Землю и угол под которым находится планета создают две версии одного и того же треугольника.
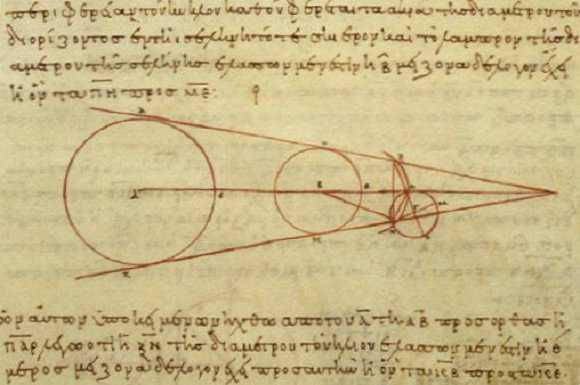
Записи древних греков о размере Луны
Используя расчеты по диаметру Земли, греки полагали, что большой треугольник будет измеряться диаметром Земли у ее основания (12875 км / 8000 миль) и составит 1390000 км (864 000 миль) в длину. Другой треугольник будет эквивалентным 2,5 диаметрам Луны и, так как треугольники пропорциональные, будет иметь высоту 2,5 орбит спутника.
Добавление двух треугольников дало бы эквивалент 3,5 Лунных орбит, которые создали бы большой треугольник и предоставили возможность (опять относительно) точного измерения расстояния между Землей и Луной. Другими словами, расстояние 1390000 км (864 000 миль), разделяем на 3,5, и в итоге получаем 397500 км (247000 миль). Не совсем точно, но весьма не плохо для древних народов!
Сегодня, ми можем получить данные о точном расстоянии к Луне с помощью времени, которое требуется свету, чтобы пройти от станции LIDAR на Земле к установленным на нашем спутнике отражателям. Этот эксперимент известен под названием Lunar Laser Ranging и стал возможным благодаря усилиям миссии Аполлон.

Lunar Laser Ranging в действии
Когда астронавты посетили Луну более сорока лет назад, они оставили ряд отражательных зеркал на ее поверхности. Когда ученые здесь на Земле стреляют лазером на Луну, свет от него отражается обратно одним из этих устройств. С каждых 100 квадриллионов фотонов, отправленных на Луну, только горстка вернуться назад, но этого достаточно, чтобы получить точную оценку.
Поскольку свет движется со скоростью почти 300000 километров (186411 миль) в секунду, все путешествие займет немного больше секунды. Вычислив точное количество времени, необходимое для света, чтобы слетать на Луну и обратно, астрономы могут определить, как далеко Луна находится в любое время, вплоть до миллиметровой точности.
С этой техникой, астрономы также обнаружили, что Луна медленно отдаляется от нас, со скоростью 3,8 см (1,5 дюйма) в год. Спустя миллионы лет, в ночном небе она будет намного меньше, чем сегодня, а за несколько миллиардов лет или около того, Луна будет визуально меньше, чем Солнце, и мы больше не сможем увидеть полных солнечных затмений.
Положение и движение Луны
Строение Луны
Поверхность Луны
o-kosmose.net
Между Землей и Луной почему-то точно умещаются все оставшиеся планеты Солнечной системы
Среднее расстояние от Земли до Луны 384 400 километров. То есть, наш естественный спутник расположился не столь уж далеко. И чтобы продемонстрировать это, специалисты НАСА «затолкали» в имеющийся промежуток оставшиеся планеты Солнечной системы. На удивление, они уместились там почти точно — с небольшими зазорами.
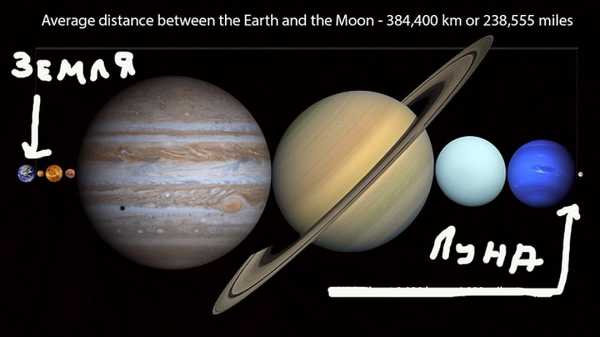
Загадочный парад планет: этот мир придуман не нами…
Можно проверить: Диаметр Меркурия 4879 километров, Венеры — 12104, Марса — 6671, Юпитера — 139822, Сатурна — 116464, Урана -50724, Нептуна — 49244 километра. Плюсуем и получаем 380008 километров. Еще бы и Плутон влез. Но он с 2006 года планетой почему-то уже не считается.
И вот теперь ученые гадают: случайно ли совпадение или так было задумано. Кстати, оно — это совпадение — не единственное. Диаметр Луны подобран так и расположена она на таком расстоянии от Солнца, что оказавшись между ним и Землей, точно прикрывает его диск. Это красивое явление называется солнечным затмением. И мы не могли бы его наблюдать, если бы наш естественный спутник был иным — меньше или больше.
— При всей абсурдности постановки вопроса он не лишен смысла на все 100 процентов, — говорит Джон Бриджес из отделения физики и астрономии Университета Лестера. — Представим себе, что планеты действительно выстроились в ряд между Луной и Землей. Что будет? Юпитер начнет поглощать их. «Всосет» все за неделю. В итоге образуется одна гигантская планета. Подобные обнаружены в других звездных системах — называются Горячие Юпитеры.

В конце останется только один. Один Горячий Юпитер как вдругих звездных системах.
По мнению ученых, у нас катастрофическое слияние планет вроде бы исключено. Но где-то, возможно, оно случалось.
Кстати, ученые прикинули, как бы выглядел небосвод, если бы на месте Луны оказалось бы что-нибудь другое. Изобразили. Вышло потрясающе.
Так выглядел бы Юпитер, если бы встал на место Луны. Тогда бы Земля оказалась бы его спутником.
И все-таки, почему все планеты Солнечной системы укладываются в промежуток между Землей и Луной? Загадка…
www.kp.ru
Расстояние до Луны
Кто не засматривался ясным погожим вечером на вечную спутницу Земли — таинственную и притягательную Луну? Издалека она кажется ровной и почти белой, но какая она на самом деле, какое расстояние до Луны? Она представляет собой естественный спутник Земли, который имеет шаровидную форму и диаметр 3480 км. Если прибегнуть к помощи телескопа, можно разглядеть ее поверхность, сплошь покрытую скалами. Учеными доказано, что на Луне полностью отсутствует атмосфера, а значит, исключена какая-либо жизнь. Гипотез происхождения Луны достаточно много, но к однозначному решению ученые еще не пришли. Возможно, что собранные факты постепенно приоткроют завесу тайны.
Расстояние от Земли до Луны, рассчитанное между их центрами, составляет 384 399 километров или 0,00257 астрономических единиц. Если сравнить его с диаметром нашей планеты, то путь до спутника составит 30 диаметров Земли. Интересен факт, что в отличие от орбиты Земли, орбита Луны эллиптическая, поэтому расстояние до Луны периодически меняет свою величину.
Во 2 веке до нашей эры об этом свойстве планеты уже знал ученый Гиппарх. Ему удалось вычислить среднее расстояние до Луны, причем почти соответствующее современному значению. Он первый рассчитал, что оно равно 30 диаметрам Земли. Другой ученый, Аристарх Самосский, в своих сочинениях «О величинах и расстояниях Солнца и Луны» еще в III в. до нашей эры попытался вычислить расстояния между этими небесными телами. Он взял за основу тот факт, что Луна имеет форму, приближенную к шаровидной, и что она светит светом, отраженным от Солнца. Он считал, когда Луна находится в определенной фазе и имеет вид полудиска, она образует геометрическую форму в виде треугольника с прямым углом. Но, к сожалению, ученый ошибся в расчетах в 20 раз, так как оказалось невозможным определить, когда именно Луна расположится в самой вершине прямого угла.
Сегодня расстояние до Луны определяется несколькими точными способами. Известен метод триангуляции из двух, самых удаленных точек на Земле. Другой метод основан на применении лазера и заключается в том, что измеряется время лазерного сигнала, посланного до Луны, а затем полученного обратно. Суть его в том, что на Луне ученые используют специально установленный уголковый отражатель. Лазерный сигнал посылают с поверхности Земли на отражатель, при этом точно устанавливается время его отправки. Посланный и отраженный на Луне свет за определенное время возвращается в телескоп. Вычислив точное время, в течение которого луч прошел расстояние от Земли до Луны и вернулся обратно, определяется расстояние от источника излучения до отражателя.
Например, в ближайшей к Земле точке орбиты расстояние до Луны составляет 363 104 км, а при удалении, точнее в апогее, оно равно 405 696 км. В итоге расстояние может отличаться почти на 12 %.
Земля и Луна не точечные тела, поэтому для определения наименьшего расстояния между ними делаем следующий расчет: из расстояния в перигее вычитаем сумму радиусов, которые равны 6378 и 1738 км. Получаемый результат и есть искомое наименьшее расстояние между точками поверхности Луны и Земли, которое равно 354 988 км.
Если бы мы отправились пешком в путь, равный расстоянию от Земли до Луны, шагая со скоростью 5 км/час без остановки, то преодолели бы его только через 9 лет. Полет на самолете со скоростью 800 км/час был бы короче, он позволил бы нам попасть на Луну через 20 дней.
В реальности преодолели расстояние до Луны американские астронавты на космическом корабле «Аполлон». Это были первые люди, которые прошлись по Луне, а произошло это значимое событие 20 июля 1969. Для этого им понадобились 3 суток. Самый быстрый способ — это лететь со скоростью света, которая равна 300 тыс. км/с, при этом Луна станет досягаемой через 1,25 световой секунды.
fb.ru

 Звёздный, или сидерический, месяц, который составляет 27 суток 7 часов 43 минуты и 11,51 секунды;
Звёздный, или сидерический, месяц, который составляет 27 суток 7 часов 43 минуты и 11,51 секунды;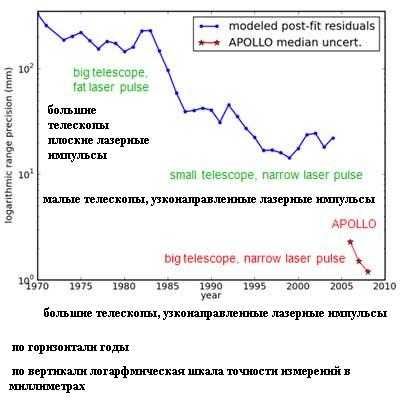 Эволюция системы Луна и Земля
Эволюция системы Луна и Земля